Powder of Dielectric Spheres

A powder composed of small spherical particles (with ε = 4 and of radius R = 100 nm) is dispersed in vacuum with a concentration of n = 10¹² particles per cm³. Find the effective dielectric constant ε' of this medium. Explain why the apparent answer,

(where V = 4πR³/3 is the volume of one particle) is wrong.

Hint: Make use of the fact that nR³ << 1. Exploit the spherical symmetry of the particles.

SOLUTION

To find the effective dielectric constant, we must first find the polarization of the spherical particles. Consider a dielectric sphere placed in a uniform electric field 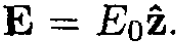Since the field at infinity is 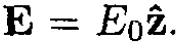and the field produced by the sphere must be a dipole field, try a solution outside the sphere:

(1)

Inside the sphere, try a field oriented in the direction of the original field E₀:

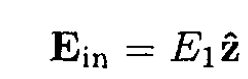(2)

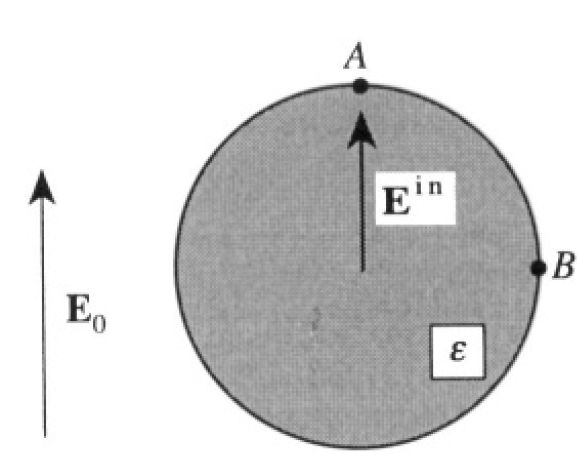
 Figure 1.1

The usual boundary conditions apply:

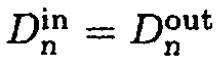(3)

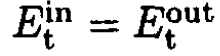(4)

Taking (3) and (4) at points A and B, respectively (see Figure 1.1),

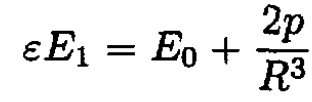(5)

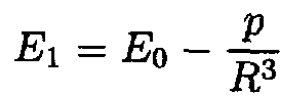(6)

Solving (5) and (6) for yields

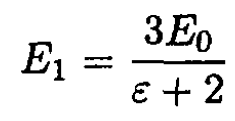(7)

so

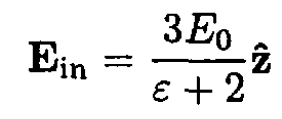
The dipole moment p is found by substituting (7) back into (6):

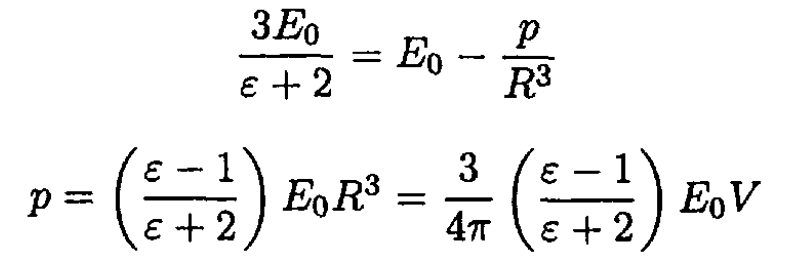
Using the condition nR² << 1 (low concentration of particles), we can disregard the interaction between them. The polarization of the medium then is given by the dipole moment per unit volume. Here, we have n dipoles per unit volume, so

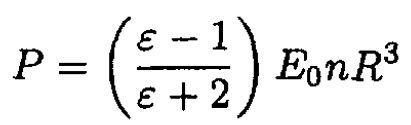(8)

Now, D = ε' E₀ = E₀ +4πP, so

(9)

The apparent but wrong answer ε' = 1 + (ε – 1)nV comes about by neglecting the shape of the particles and considering ε' as the average of the dielectric constant of free space, 1, and the dielectric constant of the spheres, ε.