
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء والفلسفة

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
العلاقة النسبوية بين الكتلة والطاقة
المؤلف:
فريدريك بوش ، دافيد جيرد
المصدر:
اساسيات الفيزياء
الجزء والصفحة:
ص 999
11-7-2016
7181
العلاقة النسبوية بين الكتلة والطاقة
أن نظرية النسبية لأينشتين تتنبأ بأن كتلة جسم ما تعتمد على مقدار سرعته، وأن هذا التأثير يصبح ملحوظاً جداً عندما تقترب تلك السرعة من سرعة الضوء c، وبما أننا لم نكن حينئذ قد تعرفنا على فروض النسبية لشرح هذا التأثير فسنفعل ذلك الآن.
تنص هذه الفروض على أنه لا يمكن تعجيل جسم إلى سرعات تزيد على سرعة الضوء. ويصطدم هذا القيد المفروض على السرعة مع قوانين نيوتن للحركة. فقوانين نيوتن تتنبأ بأن سرعة جسم ما قد تستمر في الزيادة دون قيود طالما استمرت القوة المحصلة في التأثير على الجسم:

حيث اعتبرت كتلة الجسم m ثابتة. وهذه المعادلة تخرق حد السرعة الذي يفترضه أينشتين ، لأنه بعد فترة زمنية كافية سيصبح المقدار v0 + (F/m)t أكبر من c. وقد قرر أينشتين أنه لكي يظل التوافق مع فروض النسبية ومع قانون بقاء كمية التحرك، فإن كتلة الجسم لا بد أن تتزايد بزيادة سرعته. وبهذه الطريقة يقل المقدار F/m مع زيادة t، بحيث تقترب v من القيمة الحدية للسرعة وهي c يصبح t كبيراً جداً. وقد أدت فروض أينشتين به إلى استنتاج أن العلاقة بين الكتلة والسرعة لابد أن تكون على الصورة:
(1) 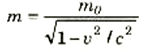
حيث يطلق على m0 كتلة السكون، وهي تساوي الكتلة التي استخدمناها في قوانين نيوتن. اما الكتلة التي تعتمد قيمتها على السرعة فتسمى الكتلة الظاهرية للجسم.
أن الكتلة الظاهرية m تظل قريبة من قيمة كتلة السكون m0 طالما كان المقدار v/c أقل من بضعة أعشار. وكلما اقتربت v من c، أي كلما v/c → 1 فإن 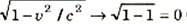 وهو ما يجعل الكتلة الظاهرية تقترب من ما لا نهاية:
وهو ما يجعل الكتلة الظاهرية تقترب من ما لا نهاية:
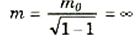
وتغير الكتلة مع السرعة، يمكن أن يستخدم لتبرير حقيقة انه لا يمكن أن يجعل أي جسم إلى سرعات تزيد على سرعة الضوء، فالكتلة اللانهائية تستلزم قوة لا نهائية لتعجيلها. وحيث أن القوى اللانهائية غير متاحة عملية، فإن الواضح أن جسماً سرعته v → c لا يمكن أن يعجل إلى سرعة الضوء، وهي السرعة التي تكون الكتلة عندها لا نهائية.
إن القوة التي تعمل على تعجيل (تسارع) جسم ما، تزود ذلك الجسم بالطاقة. ونعلم أنه عند السرعات المنخفضة يكون الشغل المبذول من جانب القوة الخالصة المطبقة مساوياً للزيادة في طاقة حركة الجسم ما لم تكن هناك تغيرات ملموسة في طاقة الوضع والشغل نتيجة الاحتكاك. ويظل هذا الأمر صحيحاً عند سرعات قريبة من c، وإن كانت طاقة حركة الجسم عندئذ ليست مجرد m0v2½، كما وأنها ليست كما قد يخمن البعض m0v2½ إذ إنها بدلاً من ذلك ستكون:
(2) 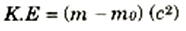
وتختصر المعادلة ((2، عندما v << c، إلى المعادلة الكلاسيكية لطاقة الحركة، KE = ½m0v2.
وعندما لا تكون على علم بسرعة الجسم ولكنك تعرف مقدار الطاقة التي أعطيت لذلك الجسم، فإن هناك وسيلة مفيدة جداً لتحديد ما إذا كان عليك أن تستخدم المعادلة (2) أو m0v2½ لحساب طاقة حركة الجسم. عليك أولاً أن تحسب طاقة كتلة سكون الجسم m0c2، ثم تقارنها بمقدار الطاقة التي أعطيت للجسم. فإذا كانت تلك الطاقة أكبر من واحد أو اثنين من عشرة أجزاء من طاقة كتلة سكون الجسم فعندئذ يقال أن الجسم " نسبوي" وعليك استخدام المعادلة (2). أما إذا كانت الطاقة المعطاة للجسم أقل من ذلك، فإن الجسم يكون عندئذ " كلاسيكي" وتكون المعادلة KE = ½m0v2 عندئذ كافية. (وكما هو الحال دائماً، فإن هذا يعتمد على الدقة التي تحتاجها في حساباتك).
تنص المعادلة (2) على أن طاقة الحركة هي الفرق بين الحدين mc2 و m0c0 وعلاوة على ذلك فهي تقتضي أن يظل الجسم محتوياً في حالة السكون (KE = 0) على بعض الطاقة الأساسية، m0c2 ، وهي ما نطلق عليه طاقة كتلة السكون. وقد تمكن أينشتين من إثبات أن علاقة شبيعة بالمعادلة (2) يمكن أن تنطبق على كل أنواع الطاقة. وقد أثبت أنه بالنسبة لأي تغير في طاقة جسم ما، فإن هناك تغيراً مناظراً في كتلة الجسم، ويعطى بالمعادلة:
(3) 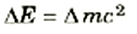
(وغالباً ما تكتب هذه العلاقة على صورة E = mc2 وهي من أشهر معادلات أينشتين).
يلاحظ أن المعادلة (3) يمكن أن تكتب أيضاً على الصورة m = ΔE/c2Δ وحيث أن c2 مقدار هائل، فإن الأمر يقتضي أن التغيرات الملموسة في الكتلة لابد لها من تغيرات ضخمة في الطاقة. والتغيرات التي نتعامل معها في عالمنا اليومي "الكلاسيكي" في مجال التفاعلات الكيميائية او التغيرات الصغير في طاقة الحركة أو طاقة الوضع أصغر من أن تتسبب في تغيرات ملموسة في الكتلة. أما عندما نرصد تغيرات في الطاقة عند حدوث تفاعلات نووية فقط، فإن تغير الكتلة يصبح واضحاً بشكل مؤثر.
 الاكثر قراءة في مواضيع عامة في النظرية النسبية
الاكثر قراءة في مواضيع عامة في النظرية النسبية
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















