
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
MODELOCKING IN THE FREQUENCY DOMAIN
المؤلف:
Mark Csele
المصدر:
FUNDAMENTALS OF LIGHT SOURCES AND LASERS
الجزء والصفحة:
p215
20-3-2016
1477
MODELOCKING IN THE FREQUENCY DOMAIN
The time-domain view of modelocking is somewhat naive in that it does not explain how this technique literally locks the phases of various longitudinal modes in the laser together. We now take a more mathematical approach to see how this can occur. When considering a practical laser it becomes apparent that many longitudinal modes (with slightly different frequencies) can oscillate simultaneously in a cavity. If these mode components are examined at any point in the tube, you’d expect to find that each of these has a different phase relative to each of the others. In a modelocked laser, all of these components are locked together in phase with each other (so, really, modelocking is phase locking). Of course, the modelocked pulse is moving down the laser cavity, each component at the same speed. Where these components interfere constructively, this is the center of the modelocked pulse with a high peak power.
This occurs at all because all modes in the laser are given equal amplification (at the same time) when the switch is open, so that energy is distributed among these modes equally. Where the modes interfere constructively (i.e., they are all in phase), the modelocked pulse peaks; where they interfere destructively, the pulse is extinguished. To see how a modelocked pulse is manifested, consider the Fourier series of the light pulse in the cavity, which consists of various (longitudinal) modes. In most practical lasers the bandwidth of the gain is wide enough to allow a number of longitudinal modes, each of slightly different frequency, to oscillate simultaneously in the laser output. A previous showed that an argon laser 90 cm long may have 31 modes in the output! This is an extreme case, but a solid-state laser such as a ruby or YAG will certainly allow many simultaneous longitudinal modes to oscillate. Modeling each wave in the laser as a sine wave, with slightly different frequencies, the amplitude of the output wave of the laser is the sum of amplitudes of each component:
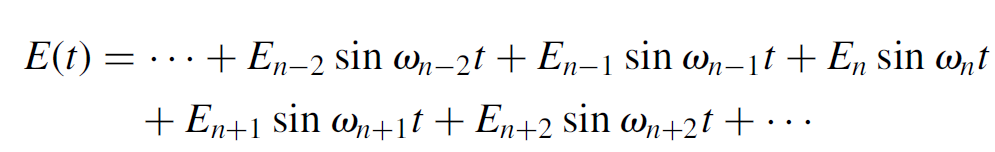 (1.1)
(1.1)
where the terms of this equation represent each component mode. For example, the component En sin ⍵nt represents a mode with frequency ⍵n, where, say 1 × 106 standing waves exist in this particular laser cavity mode (wavelength divided by cavity length). In this case, En is the amplitude of the component which follows the gain bandwidth of the lasing species. Each component of the series in the equation represents a component that is a standing wave with an integral number of waves inside the laser cavity: the (n+1) component having 1,000,001 standing waves within the cavity, the (n -1) component having 999,999 waves, and so on.
The amplitudes of each of these component waves is summed (as happens where multiple waves are present) by interference. When all component waves are in phase, constructive interference occurs, producing a large amplitude. At some point these amplitudes will sum to zero, and the resulting summed amplitude will
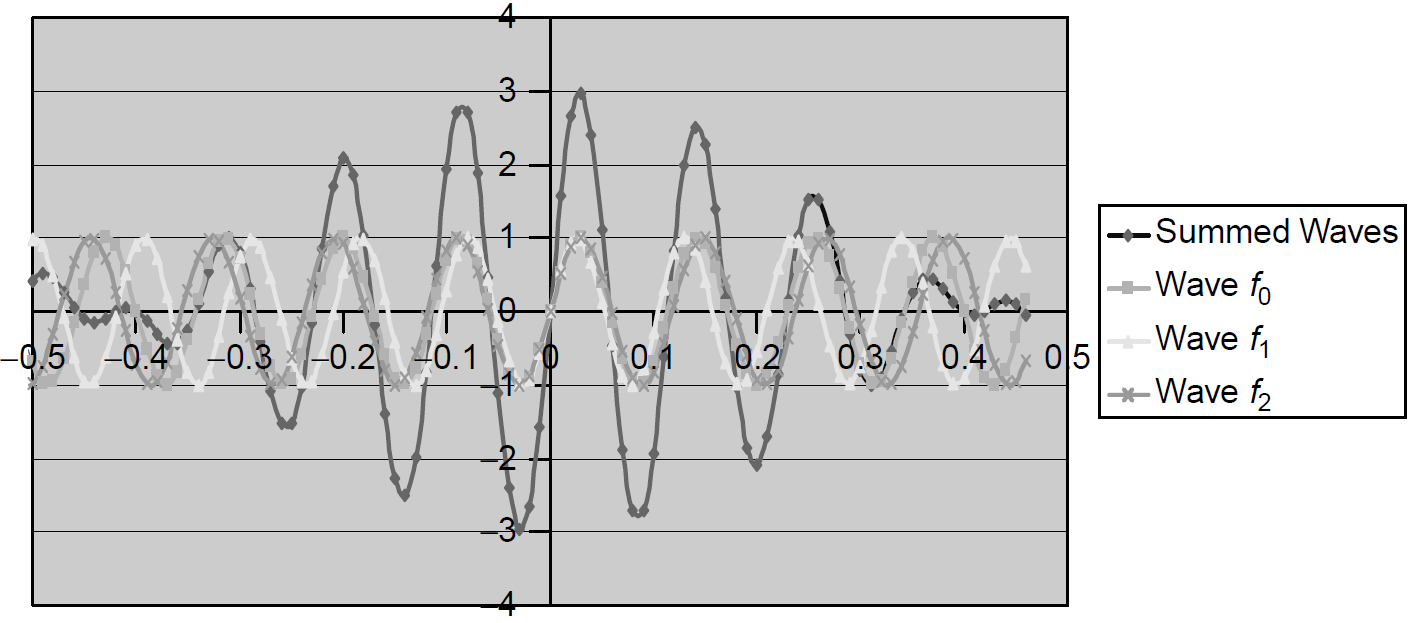
Figure 1.1. Modelocked pulse synthesis.
also be zero. This situation is outlined in Figure 1.1, where three individual modes, each with a slightly different frequency, are plotted in time. The amplitude of all three modes is also summed, revealing a pulse of large amplitude that results where the phases are the same (i.e., at the center of the figure).
By opening the Q-switch at periodic intervals, all modes in the laser are given equal amplification, which momentarily locks their phases together as shown by the central maxima in Figure 1.1. A fast, large pulse results: a modelocked pulse. If the switch is opened at regular intervals at a frequency of c/2L, the pulse continues traversing through the laser. In addition, energy builds in the upper lasing level when the pulse is not present in that area of the laser medium (in the same manner that Q-switching builds energy in the lasing medium), resulting in a high gain as the pulse passes through the laser. As the pulse is reflected from the output coupler, an output pulse results: The output from the modelocked laser thus consists of a train of extremely short pulses. A single pulse may be extracted by adding a second optical switch (such as an EO modulator) in front of the laser.
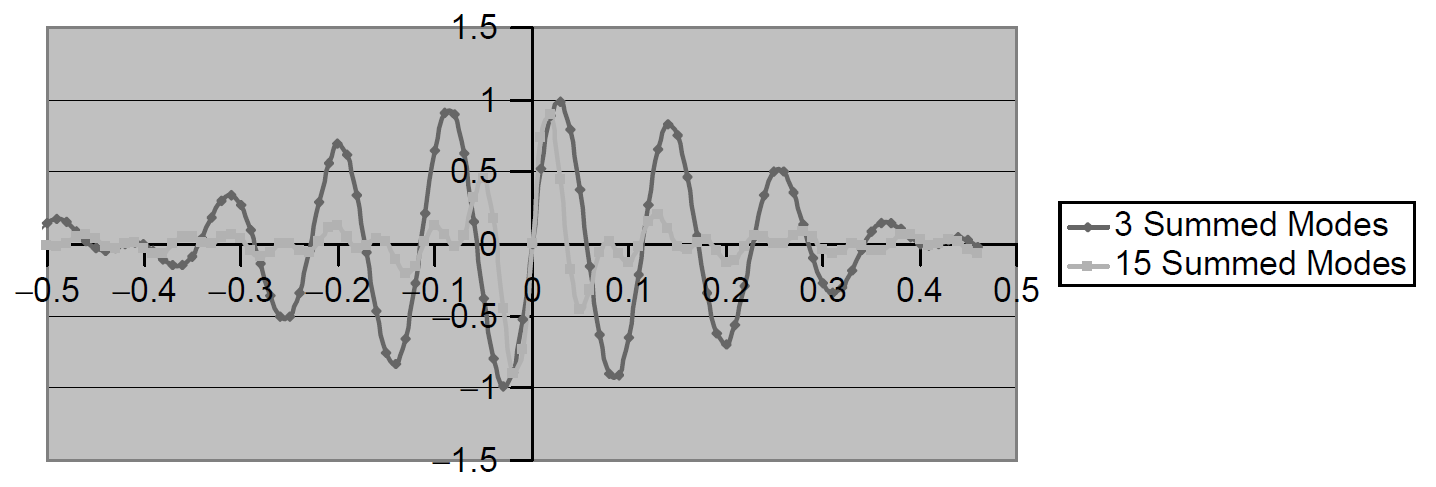
Figure 1.2. Effect of number of modes on pulse shape.
Considering that numerous longitudinal modes are required in the laser for this technique to work, the more modes that oscillate, the shorter the resulting pulse will be. A laser species with a wide spectral range will allow more modes to oscillate, and hence the pulse will be shorter. This situation is demonstrated in Figure 1.2, where the pulse shape is plotted when three and 15 component modes are summed. With three modes active, the envelope is obvious, but as more modes are summed, the envelope becomes quite narrow. In this case, the pulse appears to consist of a single wave! As more modes are allowed to exist, the pulse shape becomes shorter, which explains why the shortest pulses ever produced have been from modelocked lasers with extraordinarily wide spectral width.
For an Nd: YAG laser, the spectral width is reasonably narrow at about 0.5 nm, but Nd: YLF or Nd: glass lasers have larger spectral widths of about 5 nm, so the minimum pulse duration that may be produced is approximately 1 ps. When a laser with a larger bandwidth yet, such as a dye laser with a spectral width spanning of perhaps 100 nm, is modelocked, pulses as short as 6 fs (6 × 10-15 s) may been produced. Consider that the duration of this pulse is so short that it contains literally only a few cycles. In free space this pulse is only 9 μm long! Earlier, the impression may have been given that a narrow linewidth is always desirable; in the case of modelocking, however, a large bandwidth is required.
 الاكثر قراءة في بعض تطبيقات الليزر
الاكثر قراءة في بعض تطبيقات الليزر
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















