RATE  EQUATION  ANALYSIS  FOR  THREE- AND   FOUR-LEVEL  LASERS

         Most practical lasers feature three- and four-level atomic systems, so we shall apply the same technique used in the analysis of the two-level system to these systems. Bear in mind that many simplifications will be made to suit the model of an ideal laser, and that real lasers may have considerably more complex equations. Furthermore, we will use the concept of an optically pumped laser for simplicity (i.e., a stream of incident pump photons is used to excite lasing atoms). For other types of lasers, pump energy would be supplied in various forms, such as a DC current for a semiconductor laser diode or a flow of excited electrons for a gas laser.

         The analysis of a three-level laser, the most basic system, is methodical and progresses with an examination of energy flow into and out of each level in the system. We begin with a look at the pump level, which is populated via upward transitions from the ground state and loses population via downward decay to the ULL (denoted level 3 in Figure 1.1). It is most useful to express each level as a rate so that these may be equated for the equilibrium condition that exists when the laser is operating.

       The rate equation for the pump level can be expressed as the change of population of atoms in the pump level as follows:

 (1.1)

where W₁₃ is the probability of an atom making the transition from level 1 to level 3 and τ₃ is the decay lifetime of the pump level. The flow of energy into the pump level is described by the first half of the equation, in which (N₁ - N₃) represents the number of atoms available at the ground state to be pumped to level 3 by W₁₃ (this is the pump which, as we stated earlier, is proportional to the intensity of the incident photon stream pumping the system). Energy from the pump level flows out downward by decay to the ULL, as described by the second half of the equation (N₃/τ₃) in units of number of atoms per second. Note that the decay lifetime t3 is a total lifetime representing both the decay from level 3 to level 2 and the decay from level 3 to level 1. If each decay path 3→2 and 3 →1 has time constants τ₃₂ and τ₃₁, respectively, 1/τ₃ = 1/τ₃₂+ 1/τ₃₁.

         Following a similar line of reasoning, the rate equation for the upper lasing level can be expressed as

 (1.2)

where τ₃₂ is the decay lifetime from the pump level to the ULL and τ₂₁ is the lifetime of the ULL. Similar to the example with the pump level, energy flows into the ULL from above via decay from the pump level, the number of atoms per second being Three-Level Laser

Figure 1.1. Energy levels in three- and four-level lasers.

the population of the pump level (N₃) divided by the decay lifetime from the pump level. Note that we use the specific decay rate 1/τ₃₂ to describe the flow of energy from the pump level only to the ULL. The other path that may be possible is from the pump level directly to ground (τ₃₁), but that is undesirable and in any case, does not affect the rate equation for the ULL (except that the process may serve to depopulate the pump level, which would otherwise decay to the ULL). Energy flows out of the ULL via the transition to ground (which serves as the lower-lasing level in a three-level system such as this), which is modeled by the second part of the equation. The usefulness of these developed rate equations becomes apparent when we realize that under a steady-state condition these rates must both be equal to zero; that is, the population of each level remains constant, so the flow of energy into the level is the same as the flow of energy out of the level. By equating the rate equation for the pump level (1.1), to zero, we obtain

This may be simplified mathematically, though, since τ₃ is a small quantity (indeed, for a practical three-level laser the decay from the pump level to the upper level must be much faster than the decay from the upper to the lower lasing levels) and hence, numerically speaking, 1/τ₃ is much greater that W₁₃ so that the latter term can essentially be ignored, giving us an expression for N₃:

W₁₃τ₃N₁ = N₃     (1.3)

Not surprisingly, the population of the pump level depends on the rate of pumping itself and on the total lifetime of that level (a longer lifetime allowing higher populations to build up). We may now equate the rate of the ULL (1.2) to zero at steady state as well, stating that the population of the ULL remains constant (inversion, and hence gain, does not increase or decrease under steady-state conditions).

which yields the solution

 (1.4)

Finally, combining equations (1.3) and (1.4) and simplifying equation (1.4) by assuming that τ₃₂ =τ₃ (i.e., assuming that there is no leakage from the pump level to ground and that all atoms in the pump level decay solely to the ULL, we yield an expression for inversion now defined as N₂(t) - N₁(t(; with ΔN > 0 to signify an inversion:

  (1.5)

      In terms of the pump rate required in a three-level laser to obtain an inversion, we note that inversion does not occur with the onset of pumping. A minimum pumping rate equal to W₁₃τ₂₁ (where W₁₃ is proportional to pumping rate) is needed just to get half of the population at ground state to the upper lasing level (i.e., when ΔN = 0). The population of the upper and lower lasing levels is plotted in Figure 1.2, with inversion indicated in the shaded area. The population of the ground state (N₁) starts at N₀ at zero pump power, but as in the two-level system, each level above ground will be thermally populated according to Boltzmann statistics these populations would be negligible for most systems.

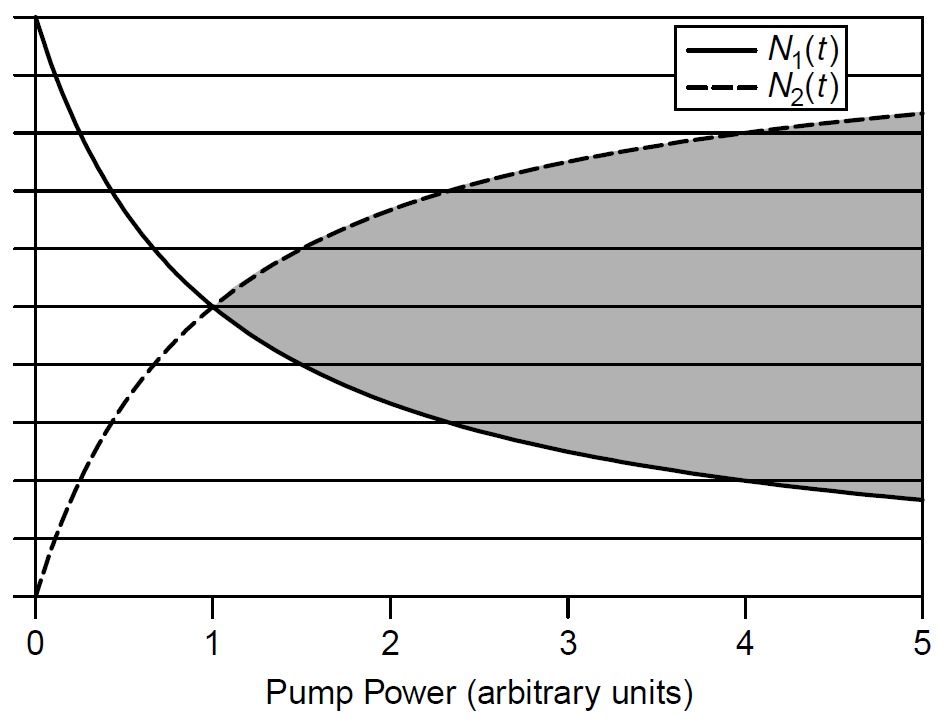
Figure 1.2. Energy-level populations for a three-level system.

       Although inversion begins at a certain pump power, even more pumping will be required to generate a sufficient inversion to create a high enough gain to overcome losses in the system (which are always significant). As we had seen earlier in the general discussion of three-level lasers (and as a specific example, the ruby laser), as a rule the lifetime of the ULL (τ21) must be much longer than the decay rate from the pump level (τ32) so that the population of the pump level will remain very low while the population of the ULL will remain very large (and hence inversion will be maintained). In the case of ruby, the 3ms lifetime of the ULL is far longer than that of the pump level, allowing an inversion to occur (especially important in a three-level laser since the LLL is ground state, which usually has a large population).

       Analysis of a four-level laser now progresses in much the same manner as that of the three-level laser, with an examination of energy flow into and out of each level in the system. We begin with a look at the pump level (denoted as level 4 in Figure 1.1). The rate equation for the pump level can be expressed as the change of population of atoms in the pump level as follows:

 (1.6)

where W₁₄ is the probability of an atom making the transition from level 1 to level 4 and τ₄ is the total lifetime of the pump level. The flow of energy into the pump level is described by the first half of the equation, in which (N₁ - N₄) represents the number of atoms available at the ground state to be pumped to level 4. Energy from the pump level flows out downward by decay to the ULL. This is described by the second half of the equation in units of number of atoms per second. Like the three-level example, note that t4 represents the total lifetime of the pump level (4), which can decay to levels 3, 2, or 1 (i.e., 1/τ₄ = 1/τ₄₃ +1/τ₄₂+ 1/ τ₄₁). In a real laser one would hope that the majority of pump atoms decay to level 3, the ULL, in order to generate an inversion; however, other paths are possible (although clearly undesirable).

     The equation for the upper lasing level can be expressed as

 (1.7)

where τ₄₃ is the decay lifetime from the pump level to the ULL and τ₃ is the lifetime of the ULL. Similar to the example with the pump level, energy flows into the ULL from above via decay from the pump level, the number of atoms per second being the population of the pump level divided by the decay lifetime from the pump level. Energy flows out of the ULL via decay, hopefully to level 2, by producing a photon of laser light, but also possibly to level 1. Finally, we can express the rate equation of the lower lasing level as

 (1.8)

where τ₄₂ is the decay lifetime from the pump level directly to the LLL, τ₃₂ the lifetime of the laser transition (ULL to LLL), and τ₂₁ the lifetime of the LLL. The first term represents a population of the LLL directly from the pump level. As mentioned previously, this is not a desirable transition but represents a loss of population from the pump level which does not contribute to laser action; worse yet, it reduces the population inversion necessary for lasing action (which is why it is shown here, as a reminder that such paths are possible). Luckily, in a practical laser system (those that work for real lasers), this term is negligible, so we shall ignore it here. The second term represents the expected route in which atoms decay from the ULL to the LLL, and the final term represents the decay from the LLL to the ground level.

      Once again, the rate equations are most useful when equated to zero under steady state conditions. Like the three-level laser, we begin with the pump level:

 (1.9)

which may be solved algebraically in terms of N₄ as

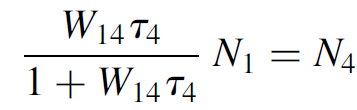 (1.10)

But the population of N₄ in a real laser will be much smaller than that of N₁, so we can simply alter equation (1.9) by eliminating one term from the left side of the equation:

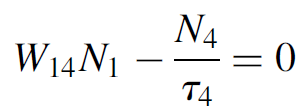 (1.11)

yielding the solution

 (1.12)

which states basically that as long as the excitation is not large enough to completely drive a large proportion of ground-state atoms to higher-energy states (the assumption we made to simplify the solution), the population of the pump level is proportional to the pump rate. Similarly, the rate equation for the ULL can be equated to zero to solve for a steady-state condition:

which yields the solution

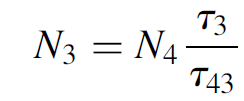 (1.13)

As we expressed earlier, in a practical four-level laser system, τ₃ (the lifetime of the ULL) is much longer than τ₄₃ (the decay rate from the pump level), so that the population of the pump level will remain very low while the population of the ULL will remain very large. Finally, we can equate the rate of the LLL to zero at steady state for the same reasons (remembering that the term N₄/τ₄₂ =0), as follows:

which yields the solution

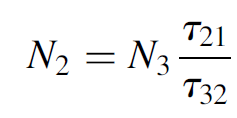 (1.14)

Finally, combining equations (1.10), (1.13), and (1.14), we obtain an expression for inversion (again, with ΔN > 0 for an inversion):

But in a practical laser the decay time from the lower lasing level (2→1) is very fast, so this term is insignificant against the first term (where τ₃ is much longer), yielding the result

 (1.15)

In other words, a population inversion results when any pump energy is supplied, as plotted in Figure 1.3, where the inversion is indicated as the shaded area.

      Unlike the three-level system, where inversion occurs only after a threshold pump rate is reached, inversion occurs immediately in a four-level system. Most

Figure 1.3. Energy-level populations for a four-level system.

common laser systems, such as the He Ne, argon, CO₂, and YAG lasers, are four level systems. Although it may appear that lasing will occur with even a small pump energy, remember that a sufficient inversion and hence gain must be built up to overcome losses in the laser before laser output will occur.