MOLECULAR  ENERGY  LEVELS

     Most transitions from gas discharges (e.g., those in a He Ne or argon-ion gas laser) have very well defined wavelengths of the type illustrated. These are electronic transitions, which involve an energy change in only electrons of the species. Precise and well defined energy states characterize these transitions, which are responsible for most visible gas laser transitions as well as those in the ultraviolet. Other energy levels possible are vibrational and rotational levels, brought on, in molecules, by various supported modes of movements of individual atoms relative to each other. In the simplest case, a diatomic molecule such as nitrogen (N₂) or hydrogen (H₂) is composed of two atoms which are free to vibrate only in certain allowed ways. When such a molecule is formed, electrons in the outer orbitals of the individual atoms are shared with neighboring atoms to form complete electron shells. In the case of a hydrogen molecule, the single electrons from each hydrogen atom combine to form a shared orbital for both atoms, this orbital belonging to the molecule as a whole rather than to an individual atom. The resulting molecule has the property that the electrons are divided symmetrically between the two hydrogen nuclei and there is no net displacement of electrical charge. As a consequence, each atom then “sees” an apparently filled n = 1 shell with two electrons in it, which leads to great stability (in other words, it will not react with other atoms to form yet other molecules), and the total energy of the molecular system is decreased when the molecule is formed (and the lowest energy state is always the most stable one). Such shared bonds, called covalent bonds, are formed, in the case of the hydrogen atom, with electrons of opposing spin, as dictated by the Pauli exclusion principle. You will recall that this principle states that no two electrons may have exactly the same set of quantum numbers, so two electrons can occupy the same molecular orbital only if they have opposite spin.

     This molecular bond is not rigid (as you may have been led to believe while using molecular model sets) but rather, is flexible and may be stretched in various ways as the atoms move. Different motions require different energies, which correspond to photon energies in the infrared region of the spectrum. Modeling a diatomic molecule as two weights attached by a spring (the covalent chemical bond between the two atoms), we may utilize kinematics to predict the behavior of this system, which resembles a simple harmonic oscillator. Allowed modes of vibration (and hence corresponding energy levels) are depicted in Figure 1.1.

     As the nuclei of the two hydrogen atoms deviate from the normal separation for a hydrogen molecule, the energy increases and the vibrational mode (denoted by v in the figure) increases. Not surprisingly, a molecule with more energy tends to vibrate more. Transitions can take place between two of these vibrational levels, resulting in a purely vibrational transition with energies corresponding to transitions in the infrared region. It is also possible to combine vibrational states such as those shown with electronic states to form hybrid vibronic levels and transitions. It is these type of transitions (from one vibronic energy level to another) that are responsible, for example, for the molecular nitrogen laser output at 337.1 nm in the ultraviolet.

    A more complex molecule, such as carbon dioxide, is depicted in the model of Figure 1.2. This molecule features a single carbon atom chemically bonded to two oxygen atoms with double covalent bonds acting as springs leading to vibrational modes each having unique levels. Such double bonds are simply the sharing of two electrons in a manner similar to that discussed previously. Of course, one would expect a double bond to be stiffer than a single bond and so have correspondingly higher vibrational energies. Several modes are shown in the figure,

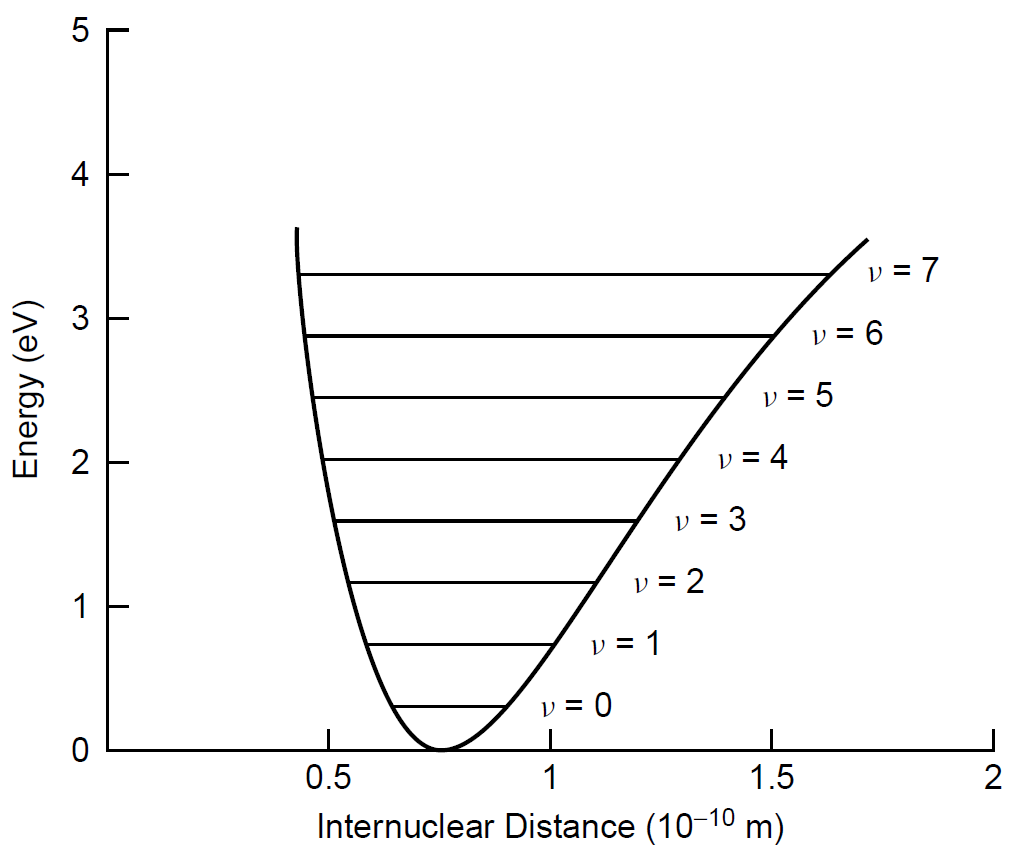
Figure 1.1. Vibrational energies in the hydrogen molecule.

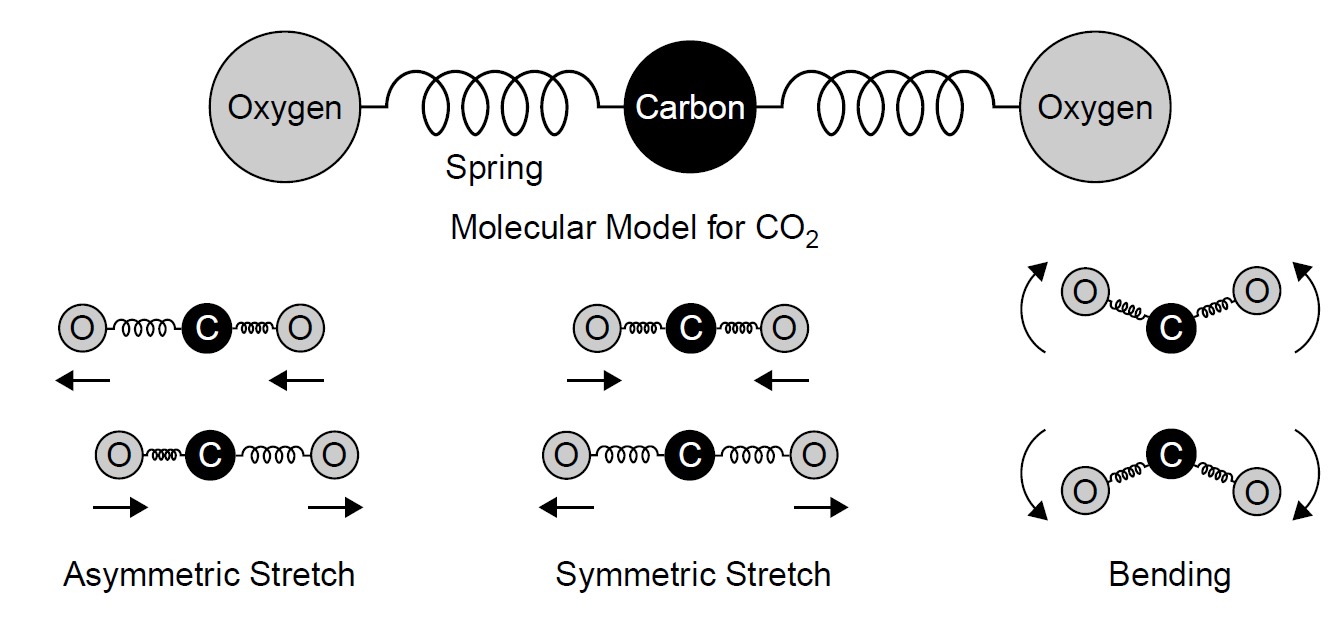
Figure 1.2. Model of the CO₂ molecule and vibrational modes.

including an asymmetric stretch (where one bonds stretches while the other compresses), symmetric stretching (where both bonds stretch or compress simultaneously), and a bending motion. Energies for such vibrational levels are again quite low (i.e., the difference between allowed energy states is quite minute), and hence transitions between allowed vibrational modes correspond to the infrared and far infrared regions of the spectrum [e.g., the carbon dioxide laser output, generated primarily by transitions between vibrational modes, is in the infrared at 10.6 μm, which corresponds to an energy of 0.117 eV; unlike the nitrogen laser, electronic levels are not involved here].

     Picturing each molecular bond as a spring between two weights, it is easy to imagine the oscillator (in a classical sense) as being confined to oscillating on certain discrete frequencies. It could oscillate at its natural resonant frequency v₀ or at twice this frequency, but not at a non-integer multiple such as 1.5 times this frequency, since this would not allow a standing wave in the spring (and would hence quickly be dampened). This is the quantized nature of atomic energy levels and applies to these types of levels as well. Oscillating at 2v₀, we expect the energy level for this vibration to be twice as large as that of v₀. In Figure 1.3, the energy levels for carbon dioxide as well as the corresponding vibrational modes are outlined. Lasing transitions (those responsible for the actual laser output) are shown in the figure between a higher-energy allowed vibrational state and two lower energy allowed vibrational states.

      The energy levels for the CO₂ molecule are assigned a three number designation that describes the vibrational mode as well as the frequency. In the case of the bending mode, two modes (010 and 020) appear in the figure. Mode 010 corresponds to a frequency of v₀, while 020 corresponds to a frequency of 2v₀, which has twice the energy of mode 010. Energy is provided to the CO₂ molecule from nitrogen in what is termed a four-level system. This pump energy level in nitrogen is also a vibrational energy level (logical since electronic levels would correspond to a much higher energy). Nitrogen (N₂) is composed of

Figure 1.3. Energy levels in the CO₂ laser.

two nitrogen atoms held together by a bond and vibrates only in certain allowed modes. The energy of one of these purely vibrational modes (not to be confused with the vibronic modes mentioned earlier in this section) corresponds closely with the upper lasing level for the CO₂ laser, so nitrogen acts as a pump.

         As well as vibrational energies (which usually correspond to transitions in the infrared), there are rotational energies involved in this system. These energies originate from various modes in which an outer atom rotates about a central atom in the case of CO₂, an oxygen atom literally rotates around the axis of the carbon and other oxygen. As one might imagine, there is a great deal of freedom to rotate in a given molecule, so there are many more possibilities for rotational modes in a large molecule than there are vibrational (although it, too, is constrained and even rotational levels are quantized).With many possibilities, rotational energy levels appear in bands of tightly clumped energy levels. Purely rotational energy levels are possible as well; these correspond to transitions in the far infrared and are seen in many organic molecules. In the CO₂ laser, vibrational energies combine with rotational energies to turn each vibrational level into a tight group of energy levels, as depicted in Figure 1.3. The result is that the two transitions of the CO₂ laser centered at 9.6 and 10.6 μm are actually a series of closely spaced spectral lines spanning the region from about 9.2 μm to almost 11 μm. We examine methods for tuning one specific line for a single-wavelength laser.

      Aside from the preceding examples of vibrational, rotational, and hybrids of these two types of levels, an energy level in a species might well involve all three types of levels. This leads to energy levels that are quite broad (we speak of energy bands at this point), so the resulting laser line is also quite broad spectrally. Dye lasers usually involve all three types of energy-level mechanisms, which leads to a continuum output over a given range. By tuning the feedback mechanism, one can selectively amplify a given wavelength: These lasers are truly tunable.