This is a traditional idea of infinity, with numbers marching on forever. Mathematics uses infinity in any which way, but care has to be taken in treating infinity like an ordinary number. It is not.

Counting

The German mathematician Georg Cantor gave us an entirely different concept of infinity. In the process, he single-handedly created a theory which has driven much of modern mathematics. The idea on which Cantor’s theory depends has to do with a primitive notion of counting, simpler than the one we use in everyday affairs.

Imagine a farmer who didn’t know about counting with numbers. How would he know how many sheep he had? Simple – when he lets his sheep out in the morning he can tell whether they are all back in the evening by pairing each sheep with a stone from a pile at the gate of his field. If there is a sheep missing there will be a stone left over. Even without using numbers, the farmer is being very mathematical. He is using the idea of a one-to-one correspondence between sheep and stones. This primitive idea has some surprising consequences.

Cantor’s theory involves sets (a set is simply a collection of objects). For example N = {1, 2, 3, 4, 5, 6, 7, 8, . . .} means the set of (positive) whole numbers. Once we have a set, we can talk about subsets, which are smaller sets within the larger set. The most obvious subsets connected with our example N are the subsets O = {1, 3, 5, 7, . . .} and E = {2, 4, 6, 8, . . .}, which are the sets of the odd and even numbers respectively. If we were to ask ‘is there the same number of odd numbers as even numbers?’ what would be our answer? Though we cannot do this by counting the elements in each set and comparing answers, the answer would still surely be ‘yes’. What is this confidence based on? – probably something like ‘half the whole numbers are odd and half are even’. Cantor would agree with the answer, but would give a different reason. He would say that every time we have an odd number, we have an even ‘mate’ next to it. The idea that both sets O and E have the same number of elements is based on the pairing of each odd number with an even number:

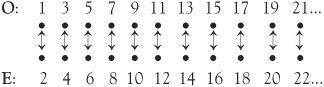
If we were to ask the further question ‘is there the same number of whole numbers as even numbers?’ the answer might be ‘no’, the argument being that the set N has twice as many numbers as the set of even numbers on its own.

The notion of ‘more’ though, is rather hazy when we are dealing with sets with an indefinite number of elements. We could do better with the one-to-one correspondence idea. Surprisingly, there is a one-to-one correspondence between N and the set of even numbers E:

We make the startling conclusion that there is the ‘same number’ of whole numbers as even numbers! This flies right in the face of the ‘common notion’ declared by the ancient Greeks; the beginning of Euclid of Alexandria’s Elements text says that ‘the whole is greater than the part’.

Cardinality

The number of elements in a set is called its ‘cardinality’. In the case of the sheep, the cardinality recorded by the farmer’s accountants is 42. The cardinality of the set {a, b, c, d, e} is 5 and this is written as card{a, b, c, d, e} = 5. So cardinality is a measure of the ‘size’ of a set. For the cardinality of the whole numbers N, and any set in a one-to-one correspondence with N, Cantor used the symbol 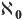(ℵ or ‘aleph’ is from the Hebrew alphabet; the symbol 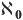is read as ‘aleph nought’). So, in mathematical language, we can write card(N) = card(O) = card(E) = .

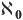Any set which can be put into a one-to-one correspondence with N is called a ‘countably infinite’ set. Being countably infinite means we can write the elements of the set down in a list. For example, the list of odd numbers is simply 1, 3, 5, 7, 9, . . . and we know which element is first, which is second, and so on.

Are the fractions countably infinite?

The set of fractions Q is a larger set than N in the sense that N can be thought of as a subset of Q. Can we write all the elements of Q down in a list? Can we devise a list so that every fraction (including negative ones) is somewhere in it? The idea that such a big set could be put in a one-to-one correspondence with N seems impossible. Nevertheless it can be done.

The way to begin is to think in two-dimensional terms. To start, we write down a row of all the whole numbers, positive and negative alternately. Beneath that we write all the fractions with 2 as denominator but we omit those which appear in the row above (like 6/₂ = 3). Below this row we write those fractions which have 3 as denominator, again omitting those which have already been recorded. We continue in this fashion, of course never ending, but knowing exactly where every fraction appears in the diagram. For example, 209/67 is in the 67th row, around 200 places to the right of 1/67.

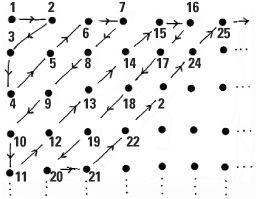
By displaying all the fractions in this way, potentially at least, we can construct a one-dimensional list. If we start on the top row and move to the right at each step we will never get to the second row. However, by choosing a devious zig-zagging route, we can be successful. Starting at 1, the promised linear list begins: 1, −1, ½, ⅓, −½, 2, −2, and follows the arrows. Every fraction, positive or negative is somewhere in the linear list and conversely its position gives its ‘mate’ in the two-dimensional list of fractions. So we can conclude that the set of fractions Q is countably infinite and write card(Q) = .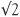

Listing the real numbers

While the set of fractions accounts for many elements on the real number line there are also real numbers like , e and a which are not fractions. These are the irrational numbers – they ‘fill in the gaps’ to give us the real number line R.

With the gaps filled in, the set R is referred to as the ‘continuum’. So, how could we make a list of the real numbers? In a move of sheer brilliance, Cantor showed that even an attempt to put the real numbers between 0 and 1 into a list is doomed to failure. This will undoubtedly come as a shock to people who are addicted to list-making, and they may indeed wonder how a set of numbers cannot be written down one after another.

Suppose you did not believe Cantor. You know that each number between 0 and 1 can be expressed as an extending decimal, for example, ½ = 0.500000000000000000. . . and 1/π = 0.31830988618379067153. . . and you would have to say to Cantor, ‘here is my list of all the numbers between 0 and 1’, which we’ll call r₁, r₂, r₃, r₄, r₅, . .. If you could not produce one then Cantor would be correct.

Imagine Cantor looks at your list and he marks in bold the numbers on the diagonal:

r₁: 0.a₁a₂a₃a₄a₅. . .

r₂: 0.b₁b₂b₃b₄b₅. . .

r₃: 0.c₁c₂c₃c₄c₅. . .

r₄: 0.d₁d₂d₃d₄d₅. . .

Cantor would have said, ‘OK, but where is the number x = x₁x₂x₃x₄x₅. . . where x₁ differs from a₁, x₂ differs from b₂, x₃ differs from c₃ working our way down the diagonal?’ His x differs from every number in your list in one decimal place and so it cannot be there. Cantor is right.

In fact, no list is possible for the set of real numbers R, and so it is a ‘larger’ infinite set, one with a ‘higher order of infinity’, than the infinity of the set of fractions Q. Big just got bigger.

the condensed idea

A shower of infinities