Two-person zero-sum games

It sounds complicated, but a two-person zero-sum game is simply one ‘played’ by two people, companies, or teams, in which one side wins what the other loses. If A wins £200 then B loses that £200; that’s what zero-sum means. There is no point in A cooperating with B – it is pure competition with only winners and losers. In ‘win–win’ language A wins £200 and B wins −£200 and the sum is 200 + (−200) = 0. This is the origin of the term ‘zero-sum’.

Let’s imagine two TV companies ATV and BTV are bidding to operate an extra news service in either Scotland or England. Each company must make a bid for one country only and they will base their decision on the projected increased size of their viewing audiences. Media analysts have estimated the increased audiences and both companies have access to their research. These are conveniently set down in a ‘payoff table’ and measured in units of a million viewers.

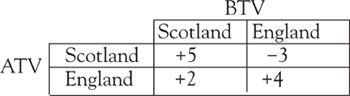
If both ATV and BTV decide to operate in Scotland then ATV will gain 5 million viewers, but BTV will lose 5 million viewers. The meaning of the minus sign, as in the payoff −3, is that ATV will lose an audience of 3 million. The + payoffs are good for ATV and the − payoffs are good for BTV.

We’ll assume the companies make their one-off decisions on the basis of the payoff table and that they make their bids simultaneously by sealed bids. Obviously both companies act in their own best interests.

If ATV chooses Scotland the worst that could happen would be a loss of 3 million; if it bids for England, the worst would be a gain of 2 million. The obvious strategy for ATV would be to choose England (row 2). It couldn’t do worse than gain 2 million viewers whatever BTV chooses. Looking at it numerically, ATV works out −3 and 2 (the row minimums) and chooses the row corresponding to the maximum of these.

BTV is in a weaker position but it can still work out a strategy that limits its potential losses and hope for a better payoff table next year. If BTV chooses Scotland (column 1) the worst that could happen would be a loss of 5 million; if it chooses England, the worst would be loss of 4 million. The safest strategy for BTV would be to choose England (column 2) for it would rather lose an audience of 4 million than 5 million. It couldn’t do worse than lose 4 million viewers whatever ATV decides.

A beautiful mind

John F. Nash (b.1928) whose troubled life was portrayed in the 2001 movie A Beautiful Mind won the Nobel Prize for Economics in 1994 for his contributions to game theory.

Nash and others extended game theory to the case of more than two players and to games where cooperation between players occurs, including ganging up on a third player. The ‘Nash equilibrium’ (like a saddle point equilibrium) gave a much broader perspective than that set down by von Neumann, resulting in a greater understanding of economic situations.

These would be the safest strategies for each player and, if followed, ATV would gain 4 million extra viewers while BTV loses them.

When is a game determined?

The following year, the two TV companies have an added option – to operate in Wales. Because circumstances have changed there is a new payoff table.

As before, the safe strategy for ATV is to choose the row which maximizes the worst that can happen. The maximum from {+1, −1, −3} is to choose Wales (row 1). The safe strategy for BTV is to choose the column which minimizes from {+4, +5, +1}. That is England (column 3).

By choosing Wales, ATV can guarantee to win no less than 1 million viewers whatever BTV does, and by choosing England (column 3), BTV can guarantee to lose no more than 1 million viewers whatever ATV does. These choices therefore represent the best strategies for each company, and in this sense the game is determined (but it is still unfair to BTV). In this game the

maximum of {+1, −1, −3} = minimum of {+4, +5, +1}

and both sides of the equation have the common value of +1. Unlike the first game, this version has a ‘saddle-point’ equilibrium of +1.

Repetitive games

The iconic repetitive game is the traditional game of ‘paper, scissors, stone’. Unlike the TV company game which was a one-off, this game is usually played half a dozen times, or a few hundred times by competitors in the annual World Championships.

In ‘paper, scissors, stone’, two players show either a hand, two fingers, or a fist, each symbolizing paper, scissors or stone. They play simultaneously on the count of three: paper draws with paper, is defeated by scissors (since scissors can cut paper), but defeats stone (because it can wrap stone). If playing ‘paper’ the payoffs are therefore 0, −1, +1, which is the top row of our completed payoff table.

There is no saddle point for this game and no obvious pure strategy to adopt. If a player always chooses the same action, say paper, the opponent will detect this and simply choose scissors to win every time. By von Neumann’s ‘minimax theorem’ there is a ‘mixed strategy’ or a way of choosing different actions based on probability.

According to the mathematics, players should choose randomly but overall the choices of paper, scissors, stone should each be made a third of the time. ‘Blind’ randomness may not always be the best course, however, as world champions have ways of choosing their strategy with a little ‘psychological’ spin. They are good at second-guessing their opponents.

When is a game not zero-sum?

Not every game is zero-sum – each player sometimes has their own separate payoff table. A famous example is the ‘prisoner’s dilemma’ designed by A.W. Tucker.

Two people, Andrew and Bertie, are picked up by the police on suspicion of highway robbery and held in separate cells so they cannot confer with each other. The payoffs, in this case jail sentences, not only depend on their individual responses to police questioning but on how they jointly respond. If Aconfesses and B doesn’t then A gets only a one year sentence (from A’s payoff table) but B is sentenced to ten years (from B’s payoff table). If A doesn’t confess but B does, the sentences go the other way around. If both confess they get four years each but if neither confesses and they both maintain their innocence they get off scot-free!

If the prisoners could cooperate they would take the optimum course of action and not confess – this would be the ‘win–win’ situation.

the condensed idea

Win–win mathematics