
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
العجلة الجاذبة المركزية
المؤلف:
فريدريك بوش ، دافيد جيرد
المصدر:
اساسيات الفيزياء
الجزء والصفحة:
الفصل 7
10-2-2016
17906
العجلة الجاذبة المركزية
تمثل حركة الجسم في مسار دائري بسرعة ثابتة المقدار موقفاً على قدر كبير من الأهمية. فمثلاً ، اعتبر حالة سيارة تسير في مسار دائري بسرعة ثابتة المقدار v، وليكن 20 m/s ، كما هو مبين بالشكل (1). بالرغم من أن مقدار سرعة السيارة 20 m/s عند الموضعين 1 و 2 وعند جميع النقط الأخرى على المسار، إلا أن السيارة تعاني عجلة معينة. ولفهم هذه العبارة يجب أن نتذكر حقيقتين: (1) مقدار السرعة والسرعة نفسها ليس نفس الشيء. (2) تعرف العجلة بأنها المعدل الزمني لتغير السرعة ( كمية متجهة) وليس المعدل الزمني لتغير مقدار السرعة (كمية غير متجهة). وحيث ان اتجاه السرعة عند الموضع 1 ليس هو اتجاهها عند الموضع 2، فإن السرعة تتغير أثناء حركة السيارة في المسار. ومن تعريف العجلة المتوسطة نجد ان العجلة المتوسطة للسيارة بين الموضعين 1 و 2 يعطي بالعلاقة:

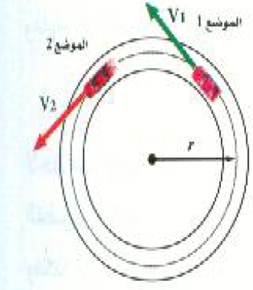
الشكل 1)): مع أن مقدار سرعة السيارة ثابت عند أي موضع على المسار فإن سرعتها تتغير باستمرار لأن اتجاه متجه السرعة ليس ثابتاً.
لتحسب الآن عجلة السيارة.
بالاستعانة بالشكل 2)) الذي يمثل نفس الموقف نلاحظ أن المركبة y لسرعة السيارة تتغير من vy عند الموضع 1 إلى - vy عند الموضع 2، بينما تظل المركبة x ثابتة عند الموضعين. من هذا نجد أنه عندما تنتقل السيارة من 1 إلى 2 ستتغير مركبة سرعة السيارة بمقدار:


الشكل ((2: لاحظ أن سرعة السيارة تتغير بمقدار – 2vy عند انتقالها من الموضع 1 إلى الموضع 2. وتبين الإشارة السالبة أن هذا التغير في الاتجاه السالب للمحور y، أي اتجاه مركز الدائرة.
كذلك فإن الزمن الذي تستغرقه السيارة للانتقال من 1 إلى 2 هو t = s/v، حيث v السرعة المماسية الثابتة المقدار للسيارة في مسارها و s طول القوس من 1 إلى 2. وحيث أن θ = s/r ، من تعريف القياس نصف القطري، إذن:

وذلك لأن s تقابل زاوية قدرها 2ϕ في هذه الحالة. وعليه :

نعلم الآن أن التغير في السرعة هو – 2vy وأن الزمن المار هو 2rϕ/v. وهكذا:

ولكننا نرى من الشكل 2)) أن vy = v sinϕ إذن :
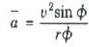
هذه هي العجلة المتوسطة للسيارة أثناء الحركة من الموضع 1 إلى الموضع 2. ولكن ما يهمنا هو قيمة العجلة اللحظية α عند أي نقطة مثل A، وللحصول على العجلة اللحظية علينا ببساطة تقليل ϕ حتى إلى قيمة صغيرة جداً. ولكن ϕ sin ϕ ≡ عندما تكون ϕ زاوية صغيرة مقدرة بالقياس نصف القطري ( استخدم حاسبة الجيب للتأكد من أن هذا صحيح)، إذن، العجلة اللحظية تكون:
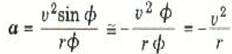
هذه هي عجلة السيارة عند مرورها بالنقطة A. وحيث ان مقدار السرعة ثابت فإن جميع النقط الواقعة على الدائرة متكافئة. ومن ثم يكون مقدار العجلة v2/r = α مهما كان موضع A على الدائرة.
لنحاول الآن إيجاد اتجاه هذه العجلة. تذكر أن اتجاه a ، طبقاً للتعريف، هو نفس اتجاه Δv وبالاستعانة بالشكل (2) نجد أن Δv= -2vyعند النقطة A، وتبين الإشارة السالبة أن Δv متجه يشير من النقطة A في اتجاه الجزء السالب من المحور y، أي اتجاه مركز الدائرة. وعليه فإن Δv ( وأيضاً a) عند A متجه يشير تجاه مركز الدائرة. ولكن النقطة A يمكن أن تكون أي نقطة نختارها على الدائرة، كما يمكن اختيار المحور y بحيث يمر بأي نقطة نختارها. ومن ثم فإن استنتاجنا الذي توصلنا إليه باختيار هذه النقطة بالذات هو استنتاج عام تماماً، وينطبق على جميع النقط الواقعة على الدائرة. وتلخيصاً لذلك نقول:
أي جسم متحرك بسرعة ثابتة المقدار في مسار دائري نصف قطره r يقع تحت تأثير عجلة تتجه نحو مركز الدائرة. هذه العجلة تسمى العجلة الجاذبية المركزية ac (حرفياً " الباحث عن المركز" )، ومقدار هذه العجلة هو:
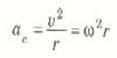
حيث استخدمنا العلاقة v = ωr
العجلة ac نصف معدل الانعطاف، يعني أنها تمثل معدل تغير اتجاه الحركة.
 الاكثر قراءة في الميكانيك
الاكثر قراءة في الميكانيك
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















