


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 5-2-2017
Date: 13-12-2015
Date: 26-1-2017
|
Maximum Entropy
Quantum field theory has too many degrees of freedom to consistently describe a gravitational theory. The main indication that we have seen of this overabundance of degrees of freedom is the fact that the horizon entropy-density is infinite in quantum field theory. The divergence arises from modes very close to the horizon. One might think that this is just an indication that a more or less conventional ultraviolet regulator is needed to render the theory consistent. But the divergent horizon entropy is not an ordinary ultraviolet phenomenon. The modes which account for the divergence are very close to the horizon and would appear to be ultra-short distance modes. But they also carry very small Rindler energy and therefore correspond to very long times to the external observer. This is an example of the weirdness of the Ultraviolet/Infrared connection.
A quantitative measure of the overabundance of degrees of freedom in QFT is provided by the Holographic Principle. This principle says that there are vastly fewer degrees of freedom in quantum gravity than in any QFT even if the QFT is regulated as, for example, it would be in lattice field theories.
The Holographic Principle is about the counting of quantum states of a system. We begin by considering a large region of space Γ. For simplicity we take the region to be a sphere. Now consider the space of states that describe arbitrary systems that can fit into Γ such that the region outside Γ is empty space. Our goal is to determine the dimensionality of that state-space. Let us consider some preliminary examples. Suppose we are dealing with a lattice of discrete spins. Let the lattice spacing be a and the volume of Γ be V .The number of spins is then V/a3 and the number of orthogonal states supported in Γ is given by
Nstates = 2V/a3 (1.1)
A second example is a continuum quantum field theory. In this case the number of quantum states will diverge for obvious reasons. We can limit the states, for example by requiring the energy density to be no larger than some bound ρmax. In this case the states can be counted using some concepts from thermodynamics. One begins by computing the thermodynamic entropy density s as a function of the energy density ρ. The total entropy is
S = s(ρ)V (1.2)
The total number of states is of order
Nstates ∼ exp S = exp s(ρmax)V (1.3)
In each case the number of distinct states is exponential in the volume V . This is a very general property of conventional local systems and represents the fact that the number of independent degrees of freedom is additive in the volume.
In counting the states of a system the entropy plays a central role. In general entropy is not really a property of a given system but also involves one's state of knowledge of the system. To define entropy we begin with some restrictions that express what we know, for example, the energy within certain limits, the angular momentum and whatever else we may know. The entropy is essentially the logarithm of the number of quantum states that satisfy the given restrictions.
There is another concept that we will call the maximum entropy. This is a property of the system. I t is the logarithm of the total number of states. In other words it is the entropy given that we know nothing about the state of the system. For the spin system the maximum entropy is
 (1.4)
(1.4)
This is typical of the maximum entropy. Whenever it exists it is proportional to the volume. More precisely it is proportional to the number of simple degrees of freedom that it takes to describe the system. Let us now consider a system that includes gravity. For definiteness we will take spacetime to be four-dimensional. Again we focus on a spherical region of space Γ with a boundary ∂Γ. The area of the boundary is A. Suppose we have a thermodynamic system with entropy S that is completely contained within Γ. The total mass of this system cannot exceed the mass of a black hole of area A or else it will be bigger than the region.
Now imagine collapsing a spherically symmetric light-like shell of matter with just the right amount of energy so that together with the original mass it forms a black hole which just fills the region. In other words the area of the horizon of the black hole is A. This is shown in Figure 1.1. The

Fig. 1.1. In-moving (zero entropy) spherical shell of photons.
result of this process is a system of known entropy, S = A/4G. But now we can use the second law of thermodynamics to tell us that the original entropy inside Γ had to be less than or equal to A/4G. In other words the maximum entropy of a region of space is proportional to its area measured in Planck units. Thus we see a radical difference between the number of states of any (regulated) quantum field theory and a theory that includes gravity.
_____________________________________________________
Space-time depiction of horizon formation
Consider the collapsing spherically symmetric shell of light-like energy depicted in Figure 1.1. As the photonic shell approaches the center, the horizon forms prior to the actual crossing of the shell. Inside of the shell, the geometry is Schwarzschild with low curvature (no black hole) prior to the shell crossing the Schwarzschild radius. However, just outside of the shell the geometry becomes increasingly curved as the Schwarzschild radius is approached (see Figure 1.2). The horizon grows until the collapsing

Fig. 1.2. Space-time depiction of radially in-moving shell of photons.
shell crosses, and a singularity forms at a later time. The energy of the infalling photonic shell Eγ has been tuned such that the collapsing shell crosses the horizon exactly at the radius R in Figure 1.1. However, at that time the system winds up with entropy

Therefore, unless the second law of thermodynamics is untrue, the entropy of any system is limited by
 (1.5)
(1.5)
The coarse grained volume in phase space cannot decrease, so this “holographic” limit must be satisfied.
____________________________________________________________
Aside: Scale of Entropy Limit
Example: To get some idea of how big a typical system must be in order to saturate the maximum entropy, consider thermal radiation at a temperature of 1000oK, which corresponds to photons of wavelength ∼10−5 cm. The number of photons Nγ in a volume of radius R satisfies Nγ ∼ V/λ3 ∼ (R(cm) ⊗ 105)3. Entropy is proportional to the number of photons, and thus one expects

Compare this with the maximum entropy calculated using the holographic limit
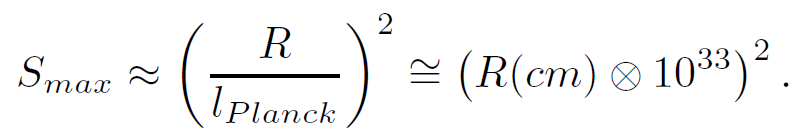 (1.6)
(1.6)
Evidently the maximum entropy will only be saturated for the photon gas when the radius is huge, R ∼ 1051 cm, considerable larger than the observable universe 1028 cm.



|
|
|
|
مخاطر خفية لمكون شائع في مشروبات الطاقة والمكملات الغذائية
|
|
|
|
|
|
|
"آبل" تشغّل نظامها الجديد للذكاء الاصطناعي على أجهزتها
|
|
|
|
|
|
|
تستخدم لأول مرة... مستشفى الإمام زين العابدين (ع) التابع للعتبة الحسينية يعتمد تقنيات حديثة في تثبيت الكسور المعقدة
|
|
|