حيثما نجد حالة تكون فيها قوة الجاذبية هي القوة الوحيدة التي تبذل شغلًا على جسيم ما، (يُفترض في الوقت الحالي، أنها ثابتة في المقدار والاتجاه)، فإن المعادلة (12–5) تكون قابلة للتطبيق. يمكن إعادة كتابة هذه المعادلة على الصورة:

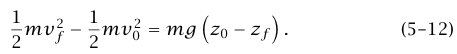
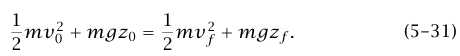
وبما أن 0 وf لحظتان اختياريتان فإننا نرى أن الكمية mv² + mgz(1/2) لها نفس القيمة في كل الأزمنة؛ أي إن:

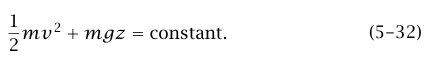
المعادلة (32–5) تتشابه في المحتوى مع المعادلة (1–5)، لكننا نتأملها بطريقة مختلفة نوعا ما. لقد أعطينا بالفعل اسمًا للكمية mv²(2/1)، وهو طاقة الحركة. المعادلة (32–5) تنص على أن مجموع طاقة الحركة والكمية mgz يظل ثابتًا أثناء الحركة؛ ولهذا فإن أي زيادة (أو نقصان) في طاقة الحركة يجب أن يكون مصاحبًا بنقصان (أو زيادة) مناظر في mgz الكمية mgz تسمى طاقة الجهد (الموضع)، والمعادلة (32–5) تنص على أن:

Kinetic energy + Potential energy = constant                (5–33)

حاصل الجمع الثابت لطاقة الحركة وطاقة الجهد (الموضع) يسمى الطاقة الميكانيكية الكلية، والمعادلة (33–5) تسمى مبدأ حفظ الطاقة. (نشير هنا إلى «الطاقة الميكانيكية» لأن هناك «أنواعًا» أخرى للطاقة. «الطاقة الميكانيكية» مصطلح يشير تحديدًا إلى الطاقة المصاحبة للموضع ومقدار سرعة مكونات نظام ما). يجب تذكَّر أننا قد أثبتنا هذا المبدأ فقط لحالة خاصة تتحقق فيها المعادلة (12–5). تمديد المبدأ إلى حالات أخرى ليس ممكنا دائما، سوف نناقش الآن الظروف التي عندها يكون مثل هذا التمديد ممكنًا.

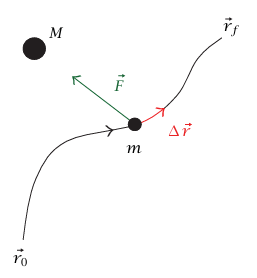
شكل 5–9 الشغل الذي تبذله الجاذبية.

نظرية الشغل والطاقة الصحيحة دائمًا (لأنها تنتج من 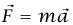 بدون فروض إضافية)، تؤكد أن:

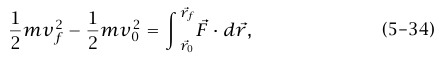
حيث الطرف الأيمن هو الشغل الكلي المبذول على الجسم لكي ينتقل من 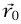إلى 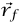. دعنا نعتبر، بوجه خاص، حالة جسيم كتلته m ومتحرك تحت تأثير الجاذبية التثاقلية لكتلة نقطية (أبقي على موضعها ثابتًا). عندئذٍ يكون:

حيث r المسافة بين M وm، و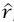 متجه وحدة يشير من M إلى m. وما يهمنا تحديدًا هو حالات تكون فيها  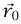و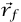 مختلفتين بما يكفي بحيث لا تُعامل  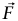على أنها ثابتة بطول المسار من 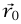إلى 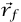 المسار الذي تقطعه m عبارة عن منحنى إلى حد ما، ويمكن تقسيمه إلى خطوات صغيرة عديدة تُمثَّل كلٌّ منها بالمتجه 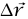. يمكن تحليل  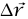إلى قطعتين؛ إحداهما توازي  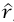والأخرى متعامدة عليه. وعندما نحسب الشغل 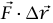، فإن القطعة  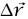التي توازي  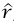هي فقط التي تسهم في حاصل الضرب القياسي. وإذا أدخلنا إحداثيات قطبية (بأخذ نقطة الأصل عند M)، فإن المتجه  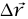يبدأ من النقطة ذات الإحداثيات القطبية (r, θ, Ф) إلى النقطة المجاورة (r + Δr, θ + Δθ, Ф + ΔФ) القطعة  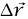بطول الاتجاه القطري هي 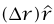؛ وبهذا نجد أن:

يوضح هذا الحساب أن الشغل المبذول بالجاذبية يعتمد فقط على نقطتي نهاية المسار؛ ومن ثُمَّ يكون هو نفسه لكل المسارات بين هاتين النقطتين (أوضحنا هذا سابقًا بفرض أن قوة الجاذبية التثاقلية ثابتة بإدخال المعادلة (37–5) في المعادلة (34–5) نجد أن:

في هذه الحالة نسمي GMm/r – طاقة الجهد التثاقلية لأن مجموع هذه الكمية وطاقة الحركة يظل ثابتًا.

(بفرض أن الأرض كروية) أن قوة الجاذبية التثاقلية التي تبذلها كتلة نقطية كتلة الأرض موضوعة عند مركز الأرض. بما أن g هي قوة الجاذبية التثاقلية لوحدة الكتلة المؤثرة على جسم ما بالقرب من سطح الأرض، فإنه ينتج أن:

حيث R نصف قطر الأرض. فضلا عن ذلك، إذا كنا نناقش حركة جسيم ما قريب من سطح الأرض، فينبغي أن نكون قادرين على توضيح أن طاقة الجهد GM_em/r – (حيث r المسافة بين m ومركز الأرض) تكافئ طاقة الجهد التي سبق تعريفها mgz. لإدراك هذا نكتب r = z + R؛ حيث z ارتفاع الجسيم فوق سطح الأرض. إذا كان z ≪ R، فإننا نستطيع استخدام نظرية ذات الحدين² لنكتب:

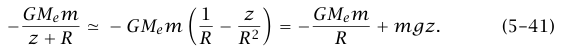
وهكذا نرى أن التعبيرين الخاصين بطاقة الجهد مختلفان فقط بثابت إضافي (جمعي) لا يعتمد على z. وحيث إنه في جميع الحسابات لا يدخل إلا فرق طاقة الموضع (الجهد) بين نقطتين، فإن التعبيرين في حقيقة الأمر متكافئان.

خاصية قوة الجاذبية التثاقلية التي مكنتنا من تعريف طاقة الجهد (أي إيجاد كمية تعتمد فقط على موضع الجسيم بحيث يظل مجموع تلك الكمية وطاقة الحركة ثابتًا) هي ما يلي: الشغل المبذول بواسطة الجاذبية على جسيم ما يتحرك بين نقطتين لا يعتمد على المسار. سوف نوضح الآن أنه حيثما يكون للقوة 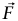 المؤثرة على جسيم ما خاصية أن الشغل لا يعتمد على المسار، فإنه يمكن تعريف طاقة الجهد.

واختصارًا للكلمات، نقدم التعريف الآتي: توصف قوة ما F بأنها محافظة إذا كان الشغل الذي تبذله 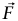 على جسيم ما يتحرك بين أي نقطتين هو نفسه لجميع المسارات بين هاتين النقطتين. لقد رأينا فعلا أن الجاذبية قوة محافظة، وأثبتنا هذا فقط للحالة التي تُعزى فيها قوة الجاذبية التثاقلية إلى جسيم مفرد لكن إذا كانت قوة الجاذبية التثاقلية تعزى إلى عدة كتل نقطية في مواضع مختلفة، فإن القوة تكون جمعية متجهيًّا (أي إن صافي القوة يكون حاصل الجمع المتجهي للقوى المبذولة بواسطة كتل مفردة)؛ وعليه يكون الشغل جمعيًّا؛ ومن ثَمَّ يكون الشغل الكلي هو نفسه لكل المسارات بين أي نقطتين محددتين.

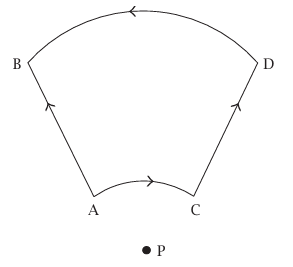
شكل 5–10: أي قوة متجهة نحو P أو مبتعدة عنها يمكن أن تكون أو لا تكون محافظة.

نفس التفسير الذي أوضح أن قوة الجاذبية التثاقلية نتيجة كتلة نقطية مفردة تكون محافظة، يوضح أيضًا أن أي قوة متجهة نحو نقطة ثابتة في المكان (أو مبتعدة عن)، ويعتمد مقدارها فقط على بعدها عن تلك النقطة، تكون قوة محافظة. ومع ذلك، إذا كانت القوة متجهة نحو نقطة ثابتة، لكن مقدارها يعتمد على البعد والاتجاه بالنسبة إلى النقطة الثابتة فإن القوة لا تكون محافظة في شكل 5–10، حيث القوة متجهة دائما نحو النقطة P، دعنا نقارن الشغل المبذول على المسار AB بالشغل المبذول على المسار ACDB (AC وDB قوسان في دائرتين مركزهما P) لا يوجد شغل مبذول على AC أو DB؛ لأن القوة تكون عمودية على الإزاحة عند كل خطوة ضئيلة. إذا كان مقدار القوة يعتمد فقط على البعد عن، فإن الشغل المبذول على المسار AB هو نفس الشكل المبذول على المسار CD لكن إذا كان مقدار القوة يعتمد على الاتجاه من P فإن الشغل المبذول على المسار AB لا يكون مساويًا للشغل المبذول على المسار CD؛ ومن ثُمَّ لا يكون الشغل المبذول على المسار AB مساويًا للشغل المبذول على المسار ACDB.

الاحتكاك مثال مهم لقوة غير محافظة. إذا ملئ حيّز ما بوسط (مثلًا هواء أو ماء) يبذل قوة معوّقة على جسم متحرك، فإن الشغل الذي تبذله هذه القوة المعوقة (الاحتكاك) يعتمد على طول المسار الذي يقطعه الجسم، ويعتمد أيضًا على مقدار السرعة التي يجتاز بها الجسم هذا المسار.

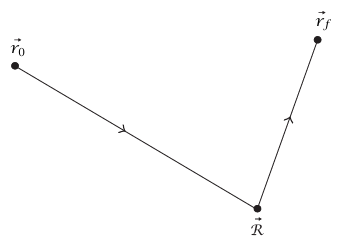
شكل 5–11: رسم تخطيطي لبرهان المعادلة (43–5).

إذا كانت قوة ما 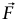 محافظة، فإن الشغل الذي تبذله  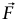على جسيم ما يتحرك من  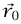إلى 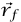 يكون دالة فقط في  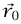و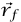 ولا يعتمد على المسار. نسمي الشغل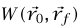

الدالة 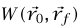 لها شكل خاص؛ فهي الفرق لدالة في 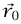ونفس الدالة في 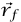. لإدراك هذا، نلتقط اختياريًا نقطة ما مثبتة  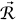(تسمى نقطة الإسناد)، ونعرف:

أي إن 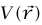 هو الشغل الذي تبذله  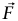على جسيم متحرك من  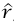إلى نقطة الإسناد. بما أن  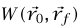لا يعتمد على المسار، فإننا نستطيع اختيار مسار يبدأ من 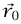حتى 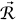 ثم يستمر من  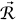إلى 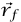؛ وبهذا نجد أ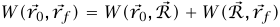ن  . لكن 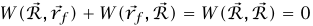 لأن أحد المسارين من  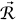إلى 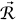 هو الطول الصفري؛ وبناءً على ذلك يكون:

إذا تحرك جسيم تحت تأثير قوة (أو قوى) محافظة بجهد مصاحب V وأيضًا تحت تأثير قوة غير محافظة (مثل الاحتكاك)، فإن نظرية الشغل والطاقة تعطي (باستخدام .E.K و.E.P لترمزا إلى طاقتي حركة وجهد):

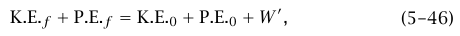
حيث W' هو الشغل الذي تبذله القوى غير المحافظة أثناء حركة الجسيم من 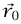إلى 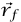. إذا كانت القوة غير المحافظة هي معوقة احتكاكية في عكس اتجاه الحركة، فإن W' < 0.

نقطة الإسناد 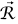 اختيارية، والتغير في نقطة الإسناد يؤدي إلى تغير طاقة الجهد عند جميع النقاط بواسطة ثابت جمعي. وحيث إن المعادلة (44–5) تشتمل على فرق طاقتي الجهد عند نقطتين، فإن الثابت الجمعي في V لن يغير أي شيء. التعريف الذي تقدمه المعادلة (42–5– يعني ضمنًا أن (0) = (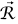V(؛ وبناءً على ذلك، إذا عرَّفنا طاقة جهد الجاذبية بأنها 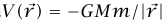، فإننا قد اخترنا نقطة الإسناد  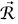نقطة لا نهائية البعد عن النقطة M. وإذا اخترنا نقطة الإسناد كنقطة على سطح الأرض، فإن 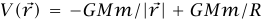. في هذه الحالة يكون الجهد عند نقاط قريبة من سطح الأرض هو mgz، وهو ما يتفق مع عملنا السابق.

مثال 5–5 (سرعة الإفلات من الأرض). بأي سرعة يجب إطلاق مقذوف من سطح الأرض لكي يُفلت (يهرب) إلى ما لا نهاية؟ (أهمل مقاومة الهواء، وتأثير دوران الأرض، وتأثير كل من الشمس والقمر).

إذا كان v_e هو مقدار سرعة المقذوف عند مغادرته الأرض، وv_∞ مقدار سرعته عندما يكون بعيدًا إلى ما لا نهاية (أي يكون بعده عن الأرض كبيرًا بأضعاف نصف قطر الأرض R). عندئذ تعني المعادلة (45–5) أن:

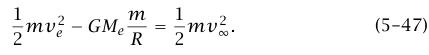
ما يهمنا هو أقل قيمة للسرعة v_e التي تتيح للمقذوف أن يصل إلى ما لا نهاية. بوضع 0 = v_∞ نجد أن 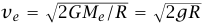. هذه السرعة تسمى سرعة الإفلات (أو الهروب من الأرض. لاحظ أن 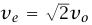؛ حيث v_e هي سرعة قمر صناعي ما في مسار دائري نصف قطره يساوي نصف قطر الأرض، عدديًّا، v_e = 2500 mi/hr, v₀ = 1800 mi/hr. أحيانًا يصف علماء الفضاء وكتاب الخيال العلمي مدار الأرض المنخفض بأنه «نصف الطريق إلى أي مكان» أو «نصف الطريق إلى ما لا نهاية؛ لأن طاقة حركة المقذوف في مدار الأرض المنخفض تساوي نصف طاقة الحركة اللازمة للهروب كليًّا من تأثير جاذبية الأرض.

_____________________________________________
هوامش

(2) National Institute of Standards and Technology, Digital library of mathematical functions, Cambridge University Press, UPH, Shaftesbury Road, Cambridge, CB2 8BS, United Kingdom, 2010.