


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
أقرأ أيضاً
التاريخ: 22-7-2019
التاريخ: 16-7-2017
التاريخ: 27-8-2019
التاريخ: 2023-03-06
|
The next subject we shall discuss is the interference of waves in both space and time. Suppose that we have two waves travelling in space. We know, of course, that we can represent a wave travelling in space by ei(ωt−kx). This might be, for example, the displacement in a sound wave. This is a solution of the wave equation provided that ω2=k2c2, where c is the speed of propagation of the wave. In this case we can write it as e−ik(x−ct), which is of the general form f(x−ct). Therefore this must be a wave which is travelling at this velocity, ω/k, and that is c and everything is all right.
Now we want to add two such waves together. Suppose we have a wave that is travelling with one frequency, and another wave travelling with another frequency. We leave to the reader to consider the case where the amplitudes are different; it makes no real difference. Thus we want to add ei(ω1t−k1x)+ei(ω2t−k2x). We can add these by the same kind of mathematics we used when we added signal waves. Of course, if c is the same for both, this is easy, since it is the same as what we did before:
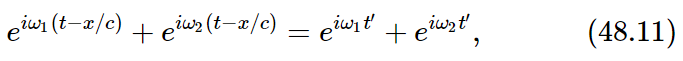
except that t′=t−x/c is the variable instead of t. So we get the same kind of modulations, naturally, but we see, of course, that those modulations are moving along with the wave. In other words, if we added two waves, but these waves were not just oscillating, but also moving in space, then the resultant wave would move along also, at the same speed.
Now we would like to generalize this to the case of waves in which the relationship between the frequency and the wave number k is not so simple. Example: material having an index of refraction., we could write k=nω/c, where n is the index of refraction. As an interesting example, for x-rays we found that the index n isA

Incidentally, we know that even when ω and k are not linearly proportional, the ratio ω/k is certainly the speed of propagation for the particular frequency and wave number. We call this ratio the phase velocity; it is the speed at which the phase, or the nodes of a single wave, would move along:

This phase velocity, for the case of x-rays in glass, is greater than the speed of light in vacuum (since n in 48.12 is less than 1), and that is a bit bothersome, because we do not think we can send signals faster than the speed of light!
What we are going to discuss now is the interference of two waves in which ω and k have a definite formula relating them. The above formula for n says that k is given as a definite function of ω. To be specific, in this particular problem, the formula for k in terms of ω is

where a=Nq2e/2ϵ0m, a constant. At any rate, for each frequency there is a definite wave number, and we want to add two such waves together.
Let us do it just as we did in Eq. (48.7):

So we have a modulated wave again, a wave which travels with the mean frequency and the mean wave number, but whose strength is varying with a form which depends on the difference frequency and the difference wave number.
Now let us take the case that the difference between the two waves is relatively small. Let us suppose that we are adding two waves whose frequencies are nearly equal; then (ω1+ω2)/2 is practically the same as either one of the ω’s, and similarly for (k1+k2)/2. Thus the speed of the wave, the fast oscillations, the nodes, is still essentially ω/k. But look, the speed of propagation of the modulation is not the same! How much do we have to change x to account for a certain amount of t? The speed of this modulation wave is the ratio

The speed of modulation is sometimes called the group velocity. If we take the case that the difference in frequency is relatively small, and the difference in wave number is then also relatively small, then this expression approaches, in the limit,

In other words, for the slowest modulation, the slowest beats, there is a definite speed at which they travel which is not the same as the phase speed of the waves—what a mysterious thing!
The group velocity is the derivative of ω with respect to k, and the phase velocity is ω/k.
Let us see if we can understand why. Consider two waves, again of slightly different wavelength, as in Fig. 48–1. They are out of phase, in phase, out of phase, and so on. Now these waves represent, really, the waves in space travelling with slightly different frequencies also. Now because the phase velocity, the velocity of the nodes of these two waves, is not precisely the same, something new happens. Suppose we ride along with one of the waves and look at the other one; if they both went at the same speed, then the other wave would stay right where it was relative to us, as we ride along on this crest. We ride on that crest and right opposite us we see a crest; if the two velocities are equal the crests stay on top of each other. But it is not so that the two velocities are really equal. There is only a small difference in frequency and therefore only a small difference in velocity, but because of that difference in velocity, as we ride along the other wave moves slowly forward, say, or behind, relative to our wave. So as time goes on, what happens to the node? If we move one wave train just a shade forward, the node moves forward (or backward) a considerable distance. That is, the sum of these two waves has an envelope, and as the waves travel along, the envelope rides on them at a different speed. The group velocity is the speed at which modulated signals would be transmitted.
If we made a signal, i.e., some kind of change in the wave that one could recognize when he listened to it, a kind of modulation, then that modulation would travel at the group velocity, provided that the modulations were relatively slow. (When they are fast, it is much more difficult to analyze.)
Now we may show (at long last), that the speed of propagation of x-rays in a block of carbon is not greater than the speed of light, although the phase velocity is greater than the speed of light. In order to do that, we must find dω/dk, which we get by differentiating (48.14): dk/dω=1/c+a/ω2c. The group velocity, therefore, is the reciprocal of this, namely,

which is smaller than c! So although the phases can travel faster than the speed of light, the modulation signals travel slower, and that is the resolution of the apparent paradox! Of course, if we have the simple case that ω=kc, then dω/dk is also c. So when all the phases have the same velocity, naturally the group has the same velocity.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|