


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
أقرأ أيضاً
التاريخ: 11-1-2016
التاريخ: 2024-03-24
التاريخ: 2024-03-30
التاريخ: 2023-10-22
|
In our analysis of light, we have gone rather far and into considerable detail. The only phenomena of any consequence associated with electromagnetic radiation that we have not discussed is what happens if radiowaves are contained in a box with reflecting walls, the size of the box being comparable to a wavelength, or are transmitted down a long tube. The phenomena of so-called cavity resonators and waveguides we shall discuss later; we shall first use another physical example—sound—and then we shall return to this subject. Except for this, the present chapter is our last consideration of the classical theory of light.
We can summarize all the effects that we shall now discuss by remarking that they have to do with the effects of moving sources. We no longer assume that the source is localized, with all its motion being at a relatively low speed near a fixed point.
We recall that the fundamental laws of electrodynamics say that, at large distances from a moving charge, the electric field is given by the formula
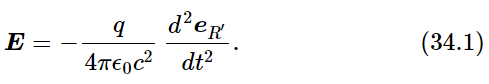
The second derivative of the unit vector eR′ which points in the apparent direction of the charge, is the determining feature of the electric field. This unit vector does not point toward the present position of the charge, of course, but rather in the direction that the charge would seem to be, if the information travels only at the finite speed c from the charge to the observer.
Associated with the electric field is a magnetic field, always at right angles to the electric field and at right angles to the apparent direction of the source, given by the formula

Until now we have considered only the case in which motions are nonrelativistic in speed, so that there is no appreciable motion in the direction of the source to be considered. Now we shall be more general and study the case where the motion is at an arbitrary velocity, and see what different effects may be expected in those circumstances. We shall let the motion be at an arbitrary speed, but of course we shall still assume that the detector is very far from the source.
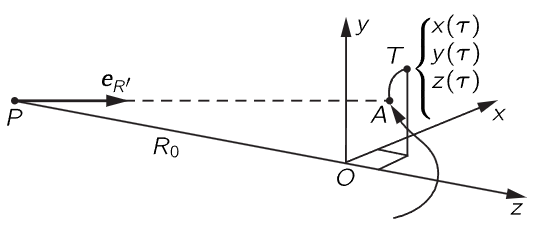
Fig. 34–1. The path of a moving charge. The true position at the time τ is at T, but the retarded position is at A.
the only things that count in d2eR′/dt2 are the changes in the direction of eR′. Let the coordinates of the charge be (x,y,z), with z measured along the direction of observation (Fig. 34–1). At a given moment in time, say the moment τ, the three components of the position are x(τ), y(τ), and z(τ). The distance R is very nearly equal to R(τ)=R0+z(τ). Now the direction of the vector eR′ depends mainly on x and y, but hardly at all upon z: the transverse components of the unit vector are x/R and y/R, and when we differentiate these components we get things like R2 in the denominator:
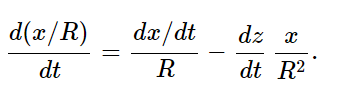
So, when we are far enough away the only terms we have to worry about are the variations of x and y. Thus we take out the factor R0 and get
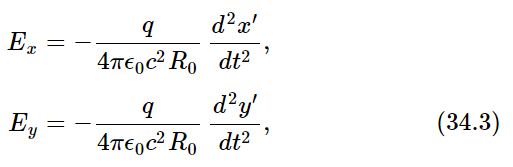
where R0 is the distance, more or less, to q; let us take it as the distance OP to the origin of the coordinates (x,y,z). Thus the electric field is a constant multiplied by a very simple thing, the second derivatives of the x- and y-coordinates. (We could put it more mathematically by calling x and y the transverse components of the position vector r of the charge, but this would not add to the clarity.)
Of course, we realize that the coordinates must be measured at the retarded time. Here we find that z(τ) does affect the retardation. What time is the retarded time? If the time of observation is called t (the time at P) then the time τ to which this corresponds at A is not the time t, but is delayed by the total distance that the light has to go, divided by the speed of light. In the first approximation, this delay is R0/c, a constant (an uninteresting feature), but in the next approximation we must include the effects of the position in the z-direction at the time τ, because if q is a little farther back, there is a little more retardation. This is an effect that we have neglected before, and it is the only change needed in order to make our results valid for all speeds.
What we must now do is to choose a certain value of t and calculate the value of τ from it, and thus find out where x and y are at that τ. These are then the retarded x and y, which we call x′ and y′, whose second derivatives determine the field. Thus τ is determined by

Now these are complicated equations, but it is easy enough to make a geometrical picture to describe their solution. This picture will give us a good qualitative feeling for how things work, but it still takes a lot of detailed mathematics to deduce the precise results of a complicated problem.



|
|
|
|
"عادة ليلية" قد تكون المفتاح للوقاية من الخرف
|
|
|
|
|
|
|
ممتص الصدمات: طريقة عمله وأهميته وأبرز علامات تلفه
|
|
|
|
|
|
|
ندوات وأنشطة قرآنية مختلفة يقيمها المجمَع العلمي في محافظتي النجف وكربلاء
|
|
|