


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
أقرأ أيضاً
التاريخ: 2024-01-07
التاريخ: 15-10-2021
التاريخ: 7-3-2016
التاريخ: 8-11-2020
|
In ideally monochromatic light, the electric field must oscillate at a definite frequency, but since the x-component and the y-component can oscillate independently at a definite frequency, we must first consider the resultant effect produced by superposing two independent oscillations at right angles to each other. What kind of electric field is made up of an x-component and a y-component which oscillate at the same frequency? If one adds to an x-vibration a certain amount of y-vibration at the same phase, the result is a vibration in a new direction in the xy-plane. Figure 33–1 illustrates the superposition of different amplitudes for the x-vibration and the y-vibration. But the resultants shown in Fig. 33–1 are not the only possibilities; in all of these cases we have assumed that the x-vibration and the y-vibration are in phase, but it does not have to be that way. It could be that the x-vibration and the y-vibration are out of phase.
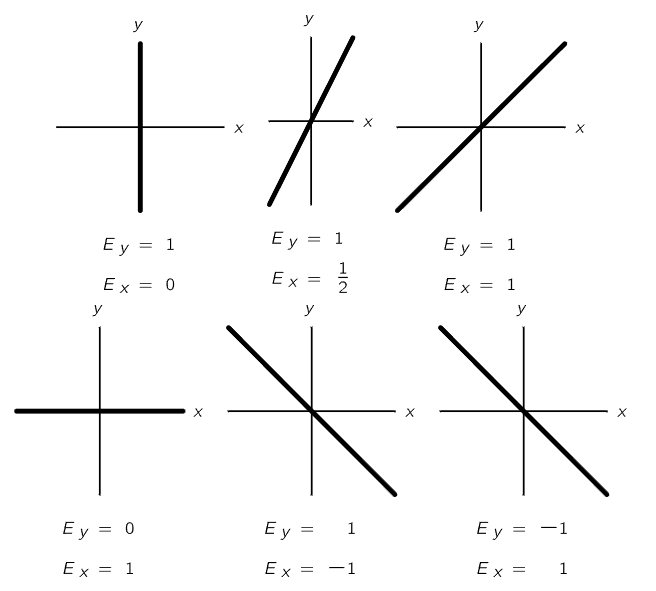
Fig. 33–1. Superposition of x-vibrations and y-vibrations in phase.
When the x-vibration and the y-vibration are not in phase, the electric field vector moves around in an ellipse, and we can illustrate this in a familiar way. If we hang a ball from a support by a long string, so that it can swing freely in a horizontal plane, it will execute sinusoidal oscillations. If we imagine horizontal x- and y-coordinates with their origin at the rest position of the ball, the ball can swing in either the x- or y-direction with the same pendulum frequency. By selecting the proper initial displacement and initial velocity, we can set the ball in oscillation along either the x-axis or the y-axis, or along any straight line in the xy-plane. These motions of the ball are analogous to the oscillations of the electric field vector illustrated in Fig. 33–1. In each instance, since the x-vibrations and the y-vibrations reach their maxima and minima at the same time, the x- and y-oscillations are in phase. But we know that the most general motion of the ball is motion in an ellipse, which corresponds to oscillations in which the x- and y-directions are not in the same phase. The superposition of x- and y-vibrations which are not in phase is illustrated in Fig. 33–2 for a variety of angles between the phase of the x-vibration and that of the y-vibration. The general result is that the electric vector moves around an ellipse. The motion in a straight line is a particular case corresponding to a phase difference of zero (or an integral multiple of π); motion in a circle corresponds to equal amplitudes with a phase difference of 90∘ (or any odd integral multiple of π/2).
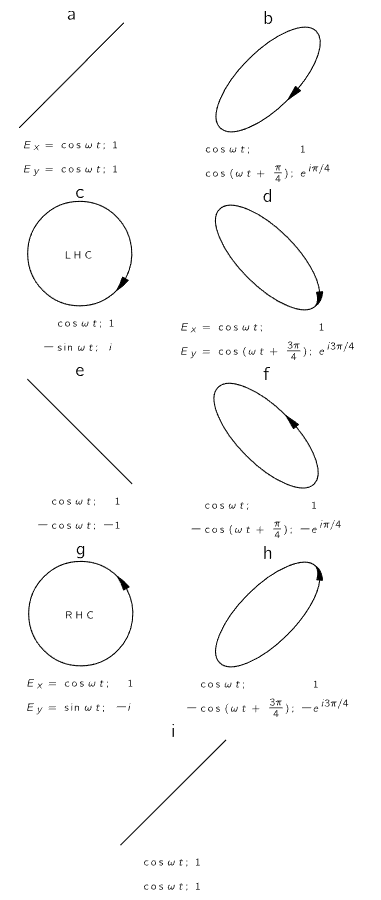
Fig. 33–2. Superposition of x-vibrations and y-vibrations with equal amplitudes but various relative phases. The components Ex and Ey are expressed in both real and complex notations.
In Fig. 33–2 we have labeled the electric field vectors in the x- and y-directions with complex numbers, which are a convenient representation in which to express the phase difference. Do not confuse the real and imaginary components of the complex electric vector in this notation with the x- and y-coordinates of the field. The x- and y-coordinates plotted in Fig. 33–1 and Fig. 33–2 are actual electric fields that we can measure. The real and imaginary components of a complex electric field vector are only a mathematical convenience and have no physical significance.
Now for some terminology. Light is linearly polarized (sometimes called plane polarized) when the electric field oscillates on a straight line; Fig. 33–1 illustrates linear polarization. When the end of the electric field vector travels in an ellipse, the light is elliptically polarized. When the end of the electric field vector travels around a circle, we have circular polarization. If the end of the electric vector, when we look at it as the light comes straight toward us, goes around in a counterclockwise direction, we call it right-hand circular polarization. Figure 33–2(g) illustrates right-hand circular polarization, and Fig. 33–2(c) shows left-hand circular polarization. In both cases the light is coming out of the paper. Our convention for labeling left-hand and right-hand circular polarization is consistent with that which is used today for all the other particles in physics which exhibit polarization (e.g., electrons). However, in some books on optics the opposite conventions are used, so one must be careful.
We have considered linearly, circularly, and elliptically polarized light, which covers everything except for the case of unpolarized light. Now how can the light be unpolarized when we know that it must vibrate in one or another of these ellipses? If the light is not absolutely monochromatic, or if the x- and y-phases are not kept perfectly together, so that the electric vector first vibrates in one direction, then in another, the polarization is constantly changing. Remember that one atom emits during 10−8 sec, and if one atom emits a certain polarization, and then another atom emits light with a different polarization, the polarizations will change every 10−8 sec. If the polarization changes more rapidly than we can detect it, then we call the light unpolarized, because all the effects of the polarization average out. None of the interference effects of polarization would show up with unpolarized light. But as we see from the definition, light is unpolarized only if we are unable to find out whether the light is polarized or not.



|
|
|
|
"عادة ليلية" قد تكون المفتاح للوقاية من الخرف
|
|
|
|
|
|
|
ممتص الصدمات: طريقة عمله وأهميته وأبرز علامات تلفه
|
|
|
|
|
|
|
قسم التربية والتعليم يكرّم الطلبة الأوائل في المراحل المنتهية
|
|
|