


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
أقرأ أيضاً
التاريخ: 11-2-2022
التاريخ: 22-5-2016
التاريخ: 2024-03-26
التاريخ: 10-7-2016
|
Now the fact that an oscillator loses a certain energy would mean that if we had a charge on the end of a spring (or an electron in an atom) which has a natural frequency ω0
, and we start it oscillating and let it go, it will not oscillate forever, even if it is in empty space millions of miles from anything. There is no oil, no resistance, in an ordinary sense; no “viscosity.” But nevertheless, it will not oscillate, as we might once have said, “forever,” because if it is charged it is radiating energy, and therefore the oscillation will slowly die out. How slowly? What is the Q of such an oscillator, caused by the electromagnetic effects, the so-called radiation resistance or radiation damping of the oscillator? The Q of any oscillating system is the total energy content of the oscillator at any time divided by the energy loss per radian:

Or (another way to write it), since dW/dϕ= (dW/dt)/(dϕ/dt)= (dW/dt)/ω,
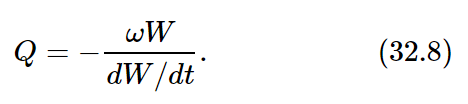
If for a given Q this tells us how the energy of the oscillation dies out, dW/dt=−(ω/Q) W, which has the solution W=W0e−ωt/Q if W0 is the initial energy (at t=0).
To find the Q for a radiator, we go back to (32.8) and use (32.6) for dW/dt.
Now what do we use for the energy W of the oscillator? The kinetic energy of the oscillator is 1/2 mv2, and the mean kinetic energy is mω2x20/4. But we remember that for the total energy of an oscillator, on the average half is kinetic and half is potential energy, and so we double our result, and find for the total energy of the oscillator

What do we use for the frequency in our formulas? We use the natural frequency ω0 because, for all practical purposes, that is the frequency at which our atom is radiating, and for m we use the electron mass me. Then, making the necessary divisions and cancellations, the formula comes down to

(In order to see it better and in a more historical form we write it using our abbreviation q2e/4πϵ0=e2, and the factor ω0/c which was left over has been written as 2π/λ.) Since Q is dimensionless, the combination e2/mec2 must be a property only of the electron charge and mass, an intrinsic property of the electron, and it must be a length. It has been given a name, the classical electron radius, because the early atomic models, which were invented to explain the radiation resistance on the basis of the force of one part of the electron acting on the other parts, all needed to have an electron whose dimensions were of this general order of magnitude. However, this quantity no longer has the significance that we believe that the electron really has such a radius. Numerically, the magnitude of the radius is

Now let us actually calculate the Q of an atom that is emitting light—let us say a sodium atom. For a sodium atom, the wavelength is roughly 6000 angstroms, in the yellow part of the visible spectrum, and this is a typical wavelength. Thus

so, the Q of an atom is of the order 108. This means that an atomic oscillator will oscillate for 108 radians or about 107 oscillations, before its energy falls by a factor 1/e. The frequency of oscillation of light corresponding to 6000 angstroms, ν=c/λ, is on the order of 1015 cycles/sec, and therefore the lifetime, the time it takes for the energy of a radiating atom to die out by a factor 1/e, is on the order of 10−8 sec. In ordinary circumstances, freely emitting atoms usually take about this long to radiate. This is valid only for atoms which are in empty space, not being disturbed in any way. If the electron is in a solid and it has to hit other atoms or other electrons, then there are additional resistances and different damping.
The effective resistance term γ in the resistance law for the oscillator can be found from the relation 1/Q=γ/ω0, and we remember that the size of γ determines how wide the resonance curve is (Fig. 23–2). Thus, we have just computed the widths of spectral lines for freely radiating atoms! Since λ=2πc/ω, we find that




|
|
|
|
مخاطر خفية لمكون شائع في مشروبات الطاقة والمكملات الغذائية
|
|
|
|
|
|
|
"آبل" تشغّل نظامها الجديد للذكاء الاصطناعي على أجهزتها
|
|
|
|
|
|
|
تستخدم لأول مرة... مستشفى الإمام زين العابدين (ع) التابع للعتبة الحسينية يعتمد تقنيات حديثة في تثبيت الكسور المعقدة
|
|
|