
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
The focal length of a spherical surface
المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
المصدر:
The Feynman Lectures on Physics
الجزء والصفحة:
Volume I, Chapter 27
2024-03-16
1706
The first and simplest situation to discuss is a single refracting surface, separating two media with different indices of refraction (Fig. 27–2). We leave the case of arbitrary indices of refraction to the student, because ideas are always the most important thing, not the specific situation, and the problem is easy enough to do in any case. So we shall suppose that, on the left, the speed is 1 and on the right it is 1/n, where n is the index of refraction. The light travels more slowly in the glass by a factor n.

Fig. 27–2. Focusing by a single refracting surface.
Now suppose that we have a point at O, at a distance s from the front surface of the glass, and another point O′ at a distance s′ inside the glass, and we desire to arrange the curved surface in such a manner that every ray from O which hits the surface, at any point P, will be bent so as to proceed toward the point O′. For that to be true, we have to shape the surface in such a way that the time it takes for the light to go from O to P, that is, the distance OP divided by the speed of light (the speed here is unity), plus n⋅O′P, which is the time it takes to go from P to O′, is equal to a constant independent of the point P. This condition supplies us with an equation for determining the surface. The answer is that the surface is a very complicated fourth-degree curve, and the student may entertain himself by trying to calculate it by analytic geometry. It is simpler to try a special case that corresponds to s→∞, because then the curve is a second-degree curve and is more recognizable. It is interesting to compare this curve with the parabolic curve we found for a focusing mirror when the light is coming from infinity.
So the proper surface cannot easily be made—to focus the light from one point to another requires a rather complicated surface. It turns out in practice that we do not try to make such complicated surfaces ordinarily, but instead we make a compromise. Instead of trying to get all the rays to come to a focus, we arrange it so that only the rays fairly close to the axis OO′ come to a focus. The farther ones may deviate if they want to, unfortunately, because the ideal surface is complicated, and we use instead a spherical surface with the right curvature at the axis. It is so much easier to fabricate a sphere than other surfaces that it is profitable for us to find out what happens to rays striking a spherical surface, supposing that only the rays near the axis are going to be focused perfectly. Those rays which are near the axis are sometimes called paraxial rays, and what we are analyzing are the conditions for the focusing of paraxial rays. We shall discuss later the errors that are introduced by the fact that all rays are not always close to the axis.
Thus, supposing P is close to the axis, we drop a perpendicular PQ such that the height PQ is h. For a moment, we imagine that the surface is a plane passing through P. In that case, the time needed to go from O to P would exceed the time from O to Q, and also, the time from P to O′ would exceed the time from Q to O′. But that is why the glass must be curved, because the total excess time must be compensated by the delay in passing from V to Q! Now the excess time along route OP is h2/2s, and the excess time on the other route is nh2/2s′
. This excess time, which must be matched by the delay in going along VQ, differs from what it would have been in a vacuum, because there is a medium present. In other words, the time to go from V to Q is not as if it were straight in the air, but it is slower by the factor n, so that the excess delay in this distance is then (n−1) VQ. And now, how large is VQ? If the point C is the center of the sphere and if its radius is R, we see by the same formula that the distance VQ is equal to h2/2R. Therefore, we discover that the law that connects the distances s and s′, and that gives us the radius of curvature R of the surface that we need, is

If we have a position O and another position O′, and want to focus light from O to O′, then we can calculate the required radius of curvature R of the surface by this formula.
Now it turns out, interestingly, that the same lens, with the same curvature R, will focus for other distances, namely, for any pair of distances such that the sum of the two reciprocals, one multiplied by n, is a constant. Thus, a given lens will (so long as we limit ourselves to paraxial rays) focus not only from O to O′, but between an infinite number of other pairs of points, so long as those pairs of points bear the relationship that 1/s+n/s′ is a constant, characteristic of the lens.
In particular, an interesting case is that in which s→∞. We can see from the formula that as one s increases, the other decreases. In other words, if point O goes out, point O′ comes in, and vice versa. As point O goes toward infinity, point O′ keeps moving in until it reaches a certain distance, called the focal length f′, inside the material. If parallel rays come in, they will meet the axis at a distance f′. Likewise, we could imagine it the other way. (Remember the reciprocity rule: if light will go from O to O′, of course it will also go from O′ to O.) Therefore, if we had a light source inside the glass, we might want to know where the focus is. In particular, if the light in the glass were at infinity (same problem) where would it come to a focus outside? This distance is called f. Of course, we can also put it the other way. If we had a light source at f and the light went through the surface, then it would go out as a parallel beam. We can easily find out what f and f′ are:
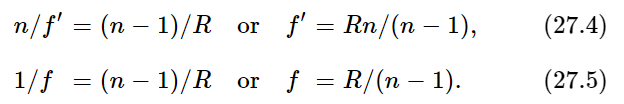
We see an interesting thing: if we divide each focal length by the corresponding index of refraction we get the same result! This theorem, in fact, is general. It is true of any system of lenses, no matter how complicated, so it is interesting to remember. We did not prove here that it is general—we merely noted it for a single surface, but it happens to be true in general that the two focal lengths of a system are related in this way. Sometimes Eq. (27.3) is written in the form

This is more useful than (27.3) because we can measure f more easily than we can measure the curvature and index of refraction of the lens: if we are not interested in designing a lens or in knowing how it got that way, but simply lift it off a shelf, the interesting quantity is f, not the n and the 1 and the R!
Now an interesting situation occurs if s becomes less than f. What happens then? If s<f, then (1/s)>(1/f), and therefore s′ is negative; our equation says that the light will focus only with a negative value of s′, whatever that means! It does mean something very interesting and very definite. It is still a useful formula, in other words, even when the numbers are negative. What it means is shown in Fig. 27–3. If we draw the rays which are diverging from O, they will be bent, it is true, at the surface, and they will not come to a focus, because O is so close in that they are “beyond parallel.” However, they diverge as if they had come from a point O′ outside the glass. This is an apparent image, sometimes called a virtual image. The image O′ in Fig. 27–2 is called a real image. If the light really comes to a point, it is a real image. But if the light appears to be coming from a point, a fictitious point different from the original point, it is a virtual image. So when s′ comes out negative, it means that O′ is on the other side of the surface, and everything is all right.
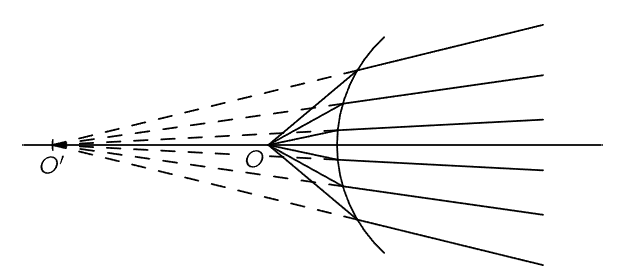
Fig. 27–3. A virtual image.
Now consider the interesting case where R is equal to infinity; then we have (1/s)+(n/s′)=0. In other words, s′=−ns, which means that if we look from a dense medium into a rare medium and see a point in the rare medium, it appears to be deeper by a factor n. Likewise, we can use the same equation backwards, so that if we look into a plane surface at an object that is at a certain distance inside the dense medium, it will appear as though the light is coming from not as far back (Fig. 27–4). When we look at the bottom of a swimming pool from above, it does not look as deep as it really is, by a factor 3/4, which is the reciprocal of the index of refraction of water.

Fig. 27–4. A plane surface re-images the light from O′ to O.
We could go on, of course, to discuss the spherical mirror. But if one appreciates the ideas involved, he should be able to work it out for himself. Therefore, we leave it to the student to work out the formula for the spherical mirror, but we mention that it is well to adopt certain conventions concerning the distances involved:
1- The object distance s is positive if the point O is to the left of the surface.
2- The image distance s′ is positive if the point O′ is to the right of the surface.
3- The radius of curvature of the surface is positive if the center is to the right of the surface.
In Fig. 27–2, for example, s, s′, and R are all positive; in Fig. 27–3, s and R are positive, but s′ is negative. If we had used a concave surface, our formula (27.3) would still give the correct result if we merely make R a negative quantity.
In working out the corresponding formula for a mirror, using the above conventions, you will find that if you put n=−1 throughout the formula (27.3) (as though the material behind the mirror had an index −1), the right formula for a mirror results!
Although the derivation of formula (27.3) is simple and elegant, using least time, one can of course work out the same formula using Snell’s law, remembering that the angles are so small that the sines of angles can be replaced by the angles themselves.
 الاكثر قراءة في مواضيع عامة في علم البصريات
الاكثر قراءة في مواضيع عامة في علم البصريات
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















