
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Reflection and refraction
المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
المصدر:
The Feynman Lectures on Physics
الجزء والصفحة:
Volume I, Chapter 26
2024-03-14
2014

Fig. 26–1. The angle of incidence is equal to the angle of reflection.
The discussion above gives enough of the basic idea of geometrical optics—now we have to go a little further into the quantitative features. Thus far we have light going only in straight lines between two points; now let us study the behavior of light when it hits various materials. The simplest object is a mirror, and the law for a mirror is that when the light hits the mirror, it does not continue in a straight line, but bounces off the mirror into a new straight line, which changes when we change the inclination of the mirror. The question for the ancients was, what is the relation between the two angles involved? This is a very simple relation, discovered long ago. The light striking a mirror travels in such a way that the two angles, between each beam and the mirror, are equal. For some reason it is customary to measure the angles from the normal to the mirror surface. Thus the so-called law of reflection is

That is a simple enough proposition, but a more difficult problem is encountered when light goes from one medium into another, for example from air into water; here also, we see that it does not go in a straight line. In the water the ray is at an inclination to its path in the air; if we change the angle θi so that it comes down more nearly vertically, then the angle of “breakage” is not as great. But if we tilt the beam of light at quite an angle, then the deviation angle is very large. The question is, what is the relation of one angle to the other? This also puzzled the ancients for a long time, and here they never found the answer! It is, however, one of the few places in all of Greek physics that one may find any experimental results listed. Claudius Ptolemy made a list of the angle in water for each of a number of different angles in air. Table 26–1 shows the angles in the air, in degrees, and the corresponding angle as measured in the water. (Ordinarily it is said that Greek scientists never did any experiments. But it would be impossible to obtain this table of values without knowing the right law, except by experiment. It should be noted, however, that these do not represent independent careful measurements for each angle but only some numbers interpolated from a few measurements, for they all fit perfectly on a parabola.)
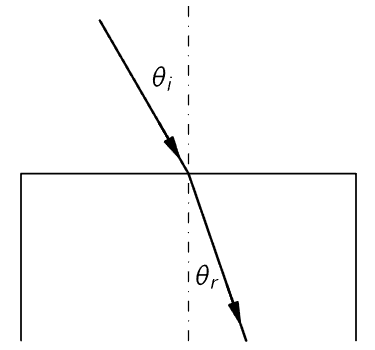
Fig. 26–2. A light ray is refracted when it passes from one medium into another.

This, then, is one of the important steps in the development of physical law: first we observe an effect, then we measure it and list it in a table; then we try to find the rule by which one thing can be connected with another. The above numerical table was made in 140 A.D., but it was not until 1621 that someone finally found the rule connecting the two angles! The rule, found by Willebrord Snell, a Dutch mathematician, is as follows: if θi is the angle in air and θr is the angle in the water, then it turns out that the sine of θi is equal to some constant multiple of the sine of θr:

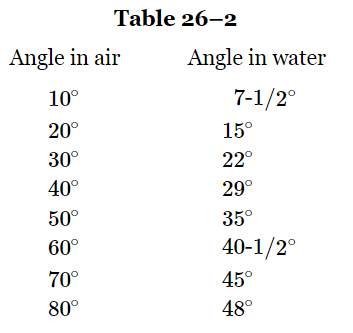
For water the number n is approximately 1.33. Equation (26.2) is called Snell’s law; it permits us to predict how the light is going to bend when it goes from air into water. Table 26–2 shows the angles in air and in water according to Snell’s law. Note the remarkable agreement with Ptolemy’s list.
 الاكثر قراءة في الضوء
الاكثر قراءة في الضوء
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















