


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
أقرأ أيضاً
التاريخ: 2024-02-28
التاريخ: 2023-08-07
التاريخ: 17-9-2019
التاريخ: 2023-02-06
|
Let us now return to our consideration of the analogy of the Lorentz transformation and rotations of the space axes. We have learned the utility of collecting together other quantities which have the same transformation properties as the coordinates, to form what we call vectors, directed lines. In the case of ordinary rotations, there are many quantities that transform the same way as x, y, and z under rotation: for example, the velocity has three components, an x, y, and z-component; when seen in a different coordinate system, none of the components is the same, instead they are all transformed to new values. But, somehow or other, the velocity “itself” has a greater reality than do any of its particular components, and we represent it by a directed line.
We therefore ask: Is it or is it not true that there are quantities which transform, or which are related, in a moving system and in a nonmoving system, in the same way as x, y, z, and t? From our experience with vectors, we know that three of the quantities, like x, y, z, would constitute the three components of an ordinary space-vector, but the fourth quantity would look like an ordinary scalar under space rotation, because it does not change so long as we do not go into a moving coordinate system. Is it possible, then, to associate with some of our known “three-vectors” a fourth object, that we could call the “time component,” in such a manner that the four objects together would “rotate” the same way as position and time in space-time? We shall now show that there is, indeed, at least one such thing (there are many of them, in fact): the three components of momentum, and the energy as the time component, transform together to make what we call a “four-vector.” In demonstrating this, since it is quite inconvenient to have to write c’s everywhere, we shall use the same trick concerning units of the energy, the mass, and the momentum, that we used in Eq. (17.4). Energy and mass, for example, differ only by a factor c2 which is merely a question of units, so we can say energy is the mass. Instead of having to write the c2, we put E=m, and then, of course, if there were any trouble, we would put in the right amounts of c so that the units would straighten out in the last equation, but not in the intermediate ones.
Thus our equations for energy and momentum are

For example, if we measure energy in electron volts, what does a mass of 1 electron volt mean? It means the mass whose rest energy is 1 electron volt, that is, m0c2 is one electron volt. For example, the rest mass of an electron is 0.511×106 eV.
Now what would the momentum and energy look like in a new coordinate system? To find out, we shall have to transform Eq. (17.6), which we can do because we know how the velocity transforms. Suppose that, as we measure it, an object has a velocity v, but we look upon the same object from the point of view of a space ship which itself is moving with a velocity u, and in that system, we use a prime to designate the corresponding thing. In order to simplify things at first, we shall take the case that the velocity v is in the direction of u. (Later, we can do the more general case.) What is v′, the velocity as seen from the space ship? It is the composite velocity, the “difference” between v and u. By the law which we worked out before,

Now let us calculate the new energy E′, the energy as the fellow in the space ship would see it. He would use the same rest mass, of course, but he would use v′ for the velocity. What we have to do is square v′, subtract it from one, take the square root, and take the reciprocal:
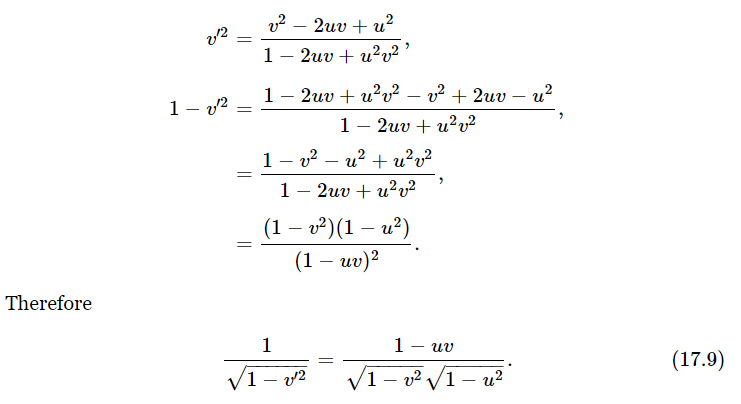
The energy E′ is then simply m0 times the above expression. But we want to express the energy in terms of the unprimed energy and momentum, and we note that

Next, we must find the new momentum p′x. This is just the energy E′ times v′, and is also simply expressed in terms of E and p:

Thus, the transformations for the new energy and momentum in terms of the old energy and momentum are exactly the same as the transformations for t′ in terms of t and x, and x′ in terms of x and t: all we have to do is, every time we see t in (17.4) substitute E, and every time we see x substitute px, and then the equations (17.4) will become the same as Eqs. (17.10) and (17.11). This would imply, if everything works right, an additional rule that p′y=py and that p′z=pz. To prove this would require our going back and studying the case of motion up and down. Actually, we did study the case of motion up and down in the last chapter. We analyzed a complicated collision and we noticed that, in fact, the transverse momentum is not changed when viewed from a moving system; so we have already verified that p′y=py and p′z=pz. The complete transformation, then, is

In these transformations, therefore, we have discovered four quantities which transform like x, y, z, and t, and which we call the four-vector momentum. Since the momentum is a four-vector, it can be represented on a space-time diagram of a moving particle as an “arrow” tangent to the path, as shown in Fig. 17–4. This arrow has a time component equal to the energy, and its space components represent its three-vector momentum; this arrow is more “real” than either the energy or the momentum, because those just depend on how we look at the diagram.

Fig. 17–4. The four-vector momentum of a particle.



|
|
|
|
مخاطر خفية لمكون شائع في مشروبات الطاقة والمكملات الغذائية
|
|
|
|
|
|
|
"آبل" تشغّل نظامها الجديد للذكاء الاصطناعي على أجهزتها
|
|
|
|
|
|
|
تستخدم لأول مرة... مستشفى الإمام زين العابدين (ع) التابع للعتبة الحسينية يعتمد تقنيات حديثة في تثبيت الكسور المعقدة
|
|
|