نظرية بورن أوبنهايمر Born - Oppenheimer

بما أن معادلة شرودينغر لجزيئة الموصوفة بالمعادلة الاتية:

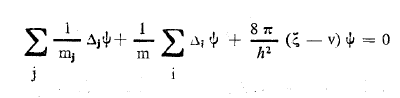..........(1)

الصعبة الحل والمعقدة لذاك نلجأ إلى افتراض أن التابع الموجي هو من الشكل:

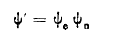
بتعويض التابع ψ في العلاقة (1) معادلة شرودينغر نجد:

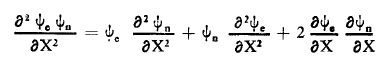
وبشكل كلي نجد:

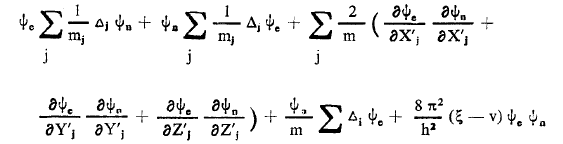
مع الأخذ بعين الإعتبار للمعادلتين الاتيتين:

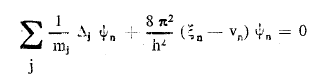
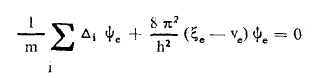
وبفرض أن :

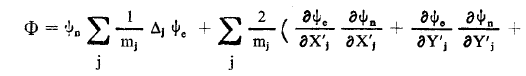
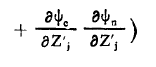
تمثل هذه العلاقة الحد الأول من معادلة شرودينغر لجزئية وهي غير معدومة باعتبار أننا استخدمنا التابع ψ وهو حل غير دقيق لهذه المعادلة اذاً يقوم تقريب بورن أو ينهايمر على أهمال Φ التي تدخل الاشتقاق من المرتبة الأولى والثانية على التابع الموجي الإلكتروني وذلك بالنسبة لاحداثيات الأنوية. وهذا يعني أن ψ_e قليل التأثير بحركة النواة أي 0 = Φ وعندئذ معادلة شرودينغر هي:

ومنه نجد :

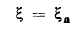
خلاصة إن ψ_e ψ_n حلول لمعادلات شرودينغر للنموذج الإلكتروني وللنموذج النووي هو حل تقريبي  لمعادلة شرودينغر لجزيئة حيث ζ و _nζ متساويتان.

اخر الاخبار

اخبار العتبة العباسية المقدسة

جمعية كشافة الكفيل: المجالس الحسينية تعلّم الفتية قيم نهضة الإمام الحسين (عليه السلام)

عَبرَ المجالس الحسينية.. المجمَع العلمي يقدّم محاضرات دينية وتلاوات قرآنية في بغداد والنجف وميسان

برعاية العتبة العباسية المقدسة.. موكب قناديل السماء يُحيي مراسم اليوم الثالث عشر من المحرّم

بعد انتهاء مراسم ذكرى دفن الأجساد الطاهرة قسم رعاية الصحن يباشر بحملة تنظيف واسعة لصحن مرقد أبي الفضل العباس (عليه السلام)

المزيد

الآخبار الصحية

اختراق علمي.. دواء يؤخر ظهور السكري من النوع الأول لسنوات

هذا ما يحدث لجسمك إن أهملت نظافة فراشك

لماذا تعتبر النساء أكثر عرضة للإصابة بألزهايمر من الرجال؟

لماذا يحذر الخبراء من الإفراط في تناول الفراولة؟

المزيد

الآخبار التكنلوجية

السيارات الكهربائية أنظف بنسبة 73% من سيارات الوقود

سيارة لوسِد الكهربائية تدخل "غينيس" بأطول مدى في العالم

نظرية جديدة تنسف كل ما نعرفه عن تشكل أول قارة في الأرض

منذ 37 ألف عام.. دراسة تكشف "أقدم أمراض" أصابت البشر

المزيد

مواضيع ذات صلة

الكشف عن الألغام والمتفجرات

الكربون .. أمير المواد وعميدها

خواص المواد النانوية

تاريخ أنابيب الكربون النانوية (History of carbon nanotubes)

الاتصال والحوار العام في تطوير تقنية النانو

نشاطات المنظمات الدولية في مجال التقنية النانوية

حالة المعارف المتصلة بمخاطر المواد النانوية

الاعتبارات الأخلاقية في التقنية النانويه

المنفعة الاجتماعية للتقنية النانوية

ما المقصود بالنانو؟

النانو تكنولوجيا.. علم وصناعة القرن الجديد

أنابيب الكربون النانوية Nanotubes Carbon