Venn Diagram

A schematic diagram used in logic theory to depict collections of sets and represent their relationships.

The Venn diagrams on two and three sets are illustrated above. The order-two diagram (left) consists of two intersecting circles, producing a total of four regions, , , , and  (the empty set, represented by none of the regions occupied). Here,  denotes the intersection of sets  and .

The order-three diagram (right) consists of three symmetrically placed mutually intersecting circles comprising a total of eight regions. The regions labeled , , and  consist of members which are only in one set and no others, the three regions labelled , , and  consist of members which are in two sets but not the third, the region  consists of members which are simultaneously in all three, and no regions occupied represents .

In general, an order- Venn diagram is a collection of  simple closed curves in the plane such that

1. The curves partition the plane into  connected regions, and

2. Each subset  of {1,2,...,n}" src="https://mathworld.wolfram.com/images/equations/VennDiagram/Inline20.svg" style="height:22px; width:93px" /> corresponds to a unique region formed by the intersection of the interiors of the curves in  (Ruskey).

Since there are  (the binomial coefficient) ways to pick  members from a total of , the number of regions in an order  Venn diagram is

(where the region outside the diagram is included in the count).

The region of intersection of the three circles  in the order three Venn diagram in the special case of the center of each being located at the intersection of the other two is a geometric shape known as a Reuleaux triangle.

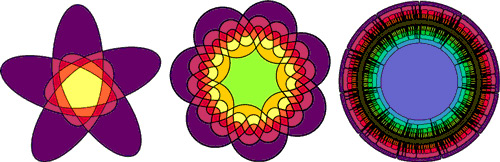
The left figure at left above shows an  Venn diagram due to Branko Grünbaum, while the attractive 7-fold rosette illustrated in the middle figure is an  Venn diagram called "Victoria" by Ruskey. The right figure shows a recently constructed symmetric Venn diagram on  due to Ruskey, Carla Savage, and Stan Wagon.

In Season 4 episode "Power" of the television crime drama NUMB3RS, mathematical genius Charles Eppes constructs a Venn diagram to determine suspects who match a particular description and have a history of violence.

 

---

REFERENCES

Cundy, H. and Rollett, A. Mathematical Models, 3rd ed. Stradbroke, England: Tarquin Pub., pp. 255-256, 1989.

Grünbaum, B. "On Venn Diagrams and the Counting of Regions." College Math. J. 15, 433-435, 1984.

Grünbaum, B. "Venn Diagrams and Independent Families of Sets." Math. Mag. 48, 12-23, 1975.

Henderson, D. W. "Venn Diagrams for More Than Four Classes." Amer. Math. Monthly 70, 424-426, 1963.

Ogilvy, C. S. "Solution to Problem E 1154." Amer. Math. Monthly 62, 584-585, 1955.Ruskey, F. "A Survey of Venn Diagrams." Electronic J. Combinatorics Dynamical Survey DS5, June 18, 2005.

 http://www.combinatorics.org/Surveys/#DS5.Ruskey, F. "Venn Diagrams." http://www.theory.csc.uvic.ca/~cos/inf/comb/SubsetInfo.html#Venn.

Ruskey, F.; Savage, C. D., and Wagon, S. "The Search for Simple Symmetric Venn Diagrams." Not. Amer. Math. Soc. 53, 1304-1311, 2006.

Venn, J. "On the Diagrammatic and Mechanical Representation of Propositions and Reasonings." Dublin Philos. Mag. J. Sci. 9, 1-18, 1880.

اخر الاخبار

اخبار العتبة العباسية المقدسة

جمعية كشافة الكفيل: المجالس الحسينية تعلّم الفتية قيم نهضة الإمام الحسين (عليه السلام)

عَبرَ المجالس الحسينية.. المجمَع العلمي يقدّم محاضرات دينية وتلاوات قرآنية في بغداد والنجف وميسان

برعاية العتبة العباسية المقدسة.. موكب قناديل السماء يُحيي مراسم اليوم الثالث عشر من المحرّم

بعد انتهاء مراسم ذكرى دفن الأجساد الطاهرة قسم رعاية الصحن يباشر بحملة تنظيف واسعة لصحن مرقد أبي الفضل العباس (عليه السلام)

المزيد

الآخبار الصحية

لكبح الجوع وخسارة الوزن.. "سر بسيط" في نظام جوكوفيتش ؟

هل يساعد الرجيم في علاج الأمراض العقلية؟

لحماية أسنان طفلك.. هذا الفيتامين يقلل خطر التسوس

أكل الطعام بسرعة.. طريق سريع إلى أمراض خطيرة

المزيد

الآخبار التكنلوجية

ما هي أفضل درجة حرارة لتكييف الهواء في السيارة؟

ذوبان الأنهار الجليدية يوقظ "عمالقة نائمة"!

9 يوليو يشهد أقصر يوم في التاريخ المسجل ؟!!

راتبه عشرات ملايين الدولارات.. زوكربرغ يخطف "عقل أبل"

المزيد

مواضيع ذات صلة

Lemma

Proof

Zeno,s Paradoxes

Unexpected Hanging Paradox

Strange Loop

Sorites Paradox

Simpson,s Paradox

Russell,s Antinomy

Paradox

Newcomb,s Paradox

Missing Dollar Paradox

Line Point Picking