Let 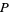 be a finite partially ordered set, then an antichain in  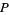is a set of pairwise incomparable elements. Antichains are also called Sperner systems in older literature (Comtet 1974).

For example, consider 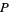 to be a family of subsets together with the subset relation (i.e.,  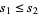if 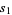 is a subset of 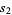). The following table gives the antichains on the set of subsets (i.e., the power set) of the 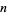-set {1,2,3,...,n}" src="https://mathworld.wolfram.com/images/equations/Antichain/Inline8.gif" style="height:16px; width:81px" /> for small .

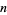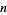	antichains
1	{{1}}" src="https://mathworld.wolfram.com/images/equations/Antichain/Inline11.gif" style="height:16px; width:40px" />
2	{{1}},{{2}},{{1},{2}},{{1,2}}" src="https://mathworld.wolfram.com/images/equations/Antichain/Inline12.gif" style="height:16px; width:171px" />
3	{{1}},{{2}},{{3}},{{1,2}}," src="https://mathworld.wolfram.com/images/equations/Antichain/Inline13.gif" style="height:16px; width:152px" />
	{{1,3}},{{2,3}},{{1},{2}},{{1},{3}}," src="https://mathworld.wolfram.com/images/equations/Antichain/Inline14.gif" style="height:16px; width:196px" />
	{{2},{3}},{{1,2,3}},{{1},{2,3}},{{1,2},{2,3}}," src="https://mathworld.wolfram.com/images/equations/Antichain/Inline15.gif" style="height:16px; width:264px" />
	{{1,2},{1,3}},{{1,2},{3}},{{2},{1,3}}," src="https://mathworld.wolfram.com/images/equations/Antichain/Inline16.gif" style="height:16px; width:218px" />
	{{2,3},{1,3}},{{1},{2},{3}},{{1,2},{2,3},{1,3}}" src="https://mathworld.wolfram.com/images/equations/Antichain/Inline17.gif" style="height:16px; width:275px" />

The number of antichains on the 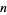-set {1,2,...,n}" src="https://mathworld.wolfram.com/images/equations/Antichain/Inline19.gif" style="height:16px; width:66px" /> for 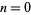, 1, 2, ..., are 1, 2, 5, 19, 167, ... (OEIS A014466). If the empty set is not considered a valid antichain, then these reduce to 0, 1, 4, 18, 166, ... (OEIS A007153; Comtet 1974, p. 273). The numbers obtained by adding one to OEIS A014466, 2, 3, 6, 20, 168, 7581, 7828354, ... (OEIS A000372), are also frequently encountered (Speciner 1972).

The number of antichains on the 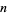-set are equal to the number of monotonic increasing Boolean functions of  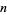variables, and also the number of free distributive lattices with  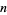generators (Comtet 1974, p. 273). Determining these numbers is known as Dedekind's problem, and the numbers in each of these sequences are sometimes called Dedekind numbers.

The partial order width of 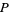 is the maximum cardinal number of an antichain in 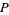. For a partial order, the size of the longest antichain is called the partial order width 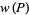. Sperner (1928) proved that the maximum size (and hence the width of the partial order) of an antichain containing  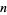elements is

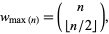where 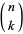 is a binomial coefficient and  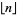is the floor function.

REFERENCES:

Agnew, R. P. "Minimax Functions, Configuration Functions, and Partitions." J. Indian Math. Soc. 24, 1-21, 1961.

Anderson, I. Combinatorics of Finite Sets. Oxford, England: Oxford University Press, p. 38, 1987.

Arocha, J. L. "Antichains in Ordered Sets" [Spanish]. Anales del Instituto de Matematicas de la Universidad Nacional Autonoma de Mexico 27, 1-21, 1987.

Berman, J. "Free Spectra of 3-Element Algebras." In Universal Algebra and Lattice Theory (Puebla, 1982) (Ed. R. S. Freese and O. C. Garcia). New York: Springer-Verlag, 1983.

Berman, J. and Koehler, P. "Cardinalities of Finite Distributive Lattices." Mitteilungen aus dem Mathematischen Seminar Giessen 121, 103-124, 1976.

Birkhoff, G. Lattice Theory, 3rd ed. Providence, RI: Amer. Math. Soc., p. 63, 1967.

Church, R. "Numerical Analysis of Certain Free Distributive Structures." Duke Math. J. 6, 732-733, 1940.

Church. "Enumeration by Rank of the Elements of the Free Distributive Lattice with Seven Generators." Not. Amer. Math. Soc. 12, 724, 1965.

Comtet, L. "Sperner Systems." §7.2 in Advanced Combinatorics: The Art of Finite and Infinite Expansions, rev. enl. ed. Dordrecht, Netherlands: Reidel, pp. 271-273, 1974.

Dedekind, R. "Über Zerlegungen von Zahlen durch ihre grössten gemeinsammen Teiler." In Gesammelte Werke, Bd. 1. pp. 103-148, 1897.

Erdős, P.; Ko, Chao; and Rado, R. "Intersection Theorems for Systems of Finite Sets." Quart. J. Math. Oxford 12, 313-320, 1961.

Gilbert, E. N. "Lattice Theoretic Properties of Frontal Switching Networks." J. Math. Phys. 33, 57-97, 1954.

Hansel, G. "Problèmes de dénombrement et d'évaluation de bornes concernant les éléments du trellis distributif libre." Publ. Inst. Statist. Univ. Paris 16, 163-294, 1967.

Harrison, M. A. Introduction to Switching and Automata Theory. New York: McGraw-Hill, p. 188, 1965.

Hilton, A. J. W. and Milner, E. C. "Some Intersection Theorems of Systems of Finite Sets." Quart. J. Math. Oxford 18, 369-384, 1967.

Katona, G. "On a Conjecture of Erdős and a Stronger Form of Sperner's Theorem." Studia Sci. Math. Hung. 1, 59-63, 1966.

Katona, G. "A Theorem of Finite Sets." In Theory of Graphs, Proceedings of the Colloquium Held at Tihany, Hungary, September 1966 (Ed. P. Erdős and G. Katona). New York: Academic Press, pp. 187-207, 1968.

Kleitman, D. "A Conjecture of Erdős-Katona on Commensurable Pairs Among Subsets of a 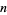-Set." In Theory of Graphs, Proceedings of the Colloquium Held at Tihany, Hungary, September 1966 (Ed. P. Erdős and G. Katona). New York: Academic Press, pp. 215-218, 1968.

Kleitman, D. "On Dedekind's Problem: The Number of Monotone Boolean Functions." Proc. Amer. Math. Soc. 21, 677-682, 1969.

Kleitman, D. and Markowsky, G. "On Dedekind's Problem: The Number of Isotone Boolean Functions. II." Trans. Amer. Math. Soc. 213, 373-390, 1975.

Lunnon, W. F. "The IU Function: The Size of a Free Distributive Lattice." In Combinatorial Mathematics and Its Applications: Proceedings of a conference held at the Mathematical Institute, Oxford, from 7-10 July, 1969 (Ed. D. J. A. Welsh). New York: Academic Press, pp. 173-181, 1971.

Mešalkin, L. D. "A Generalization of Sperner's Theorem on the Number of Subsets of a Finite Set." Theory Prob. 8, 203-204, 1963.

Milner, E. C. "A Combinatorial Theorem on Systems of Sets." J. London Math. Soc. 43, 204-206, 1968.

Muroga, S. Threshold Logic and Its Applications. New York: Wiley, p. 38 and 214, 1971.

Rivière, N. M. "Recursive Formulas on Free Distributive Lattices." J. Combin. Th. 5, 229-234, 1968.

Shapiro. "On the Counting Problem for Monotone Boolean Functions." Comm. Pure Appl. Math. 23, 299-312, 1970.

Skiena, S. Implementing Discrete Mathematics: Combinatorics and Graph Theory with Mathematica. Reading, MA: Addison-Wesley, p. 241, 1990.

Sloane, N. J. A. Sequences A006826/M2469, A007153/M3551, and A014466 in "The On-Line Encyclopedia of Integer Sequences."

Speciner, M. Item 18 in Beeler, M.; Gosper, R. W.; and Schroeppel, R. HAKMEM. Cambridge, MA: MIT Artificial Intelligence Laboratory, Memo AIM-239, p. 10, Feb. 1972. http://www.inwap.com/pdp10/hbaker/hakmem/boolean.html#item18.

Sperner, E. "Ein Satz über Untermengen einer endlichen Menge." Math. Z. 27, 544-548, 1928.

Ward, M. "Note on the Order of the Free Distributive Lattice." Bull. Amer. Math. Soc. 52, 423, 1946.

Yamamoto, K. "Logarithmic Order of Free Distributive Lattice." J. Math. Soc. Japan 6, 343-353, 1954.

اخر الاخبار

اخبار العتبة العباسية المقدسة

قسم الشعائر يواصل تحضيراته لتنظيم عمل المواكب الحسينية في زيارة الأربعين

قسم شؤون المعارف يناقش تحضيرات المؤتمر العلمي الأول لمركز تراث البصرة

قسم الشؤون الفكرية يقيم دورة تطويرية لملاكات هيأة المساءلة والعدالة في الأرشفة الإلكترونية

المجمع العلمي ينظم مجلس عزاء في قضاء الهندية

المزيد

الآخبار الصحية

نصائح عملية للحد من التعرق المفرط في الصيف

أطباء يحذرون: مكمل غذائي شائع قد يدمر الجهاز العصبي

تحذير طبي من تأثير جانبي "غير متوقع" لحقن التخسيس

حمامات الثلج قد تكون خطيرة وأحيانا مميتة.. ما السبب؟

المزيد

الآخبار التكنلوجية

أكبر جدارية شمسية في العالم تدخل موسوعة غينيس.. مشروع ضخم

تسارع دوران الأرض يثير القلق.. وتحذيرات من "كوارث محتملة" ؟

"سوذبيز" تطرح أكبر قطعة من المريخ على الأرض في مزاد علني

أوبن أيه آي تعتزم إطلاق متصفح إنترنت يعمل بالذكاء الاصطناعي

المزيد