


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 23-12-2021
Date: 16-1-2022
Date: 11-1-2022
|
Let 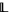 be a nontrivial bounded lattice (or a complemented lattice, etc.). Then
be a nontrivial bounded lattice (or a complemented lattice, etc.). Then 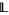 is a tight lattice if every proper tolerance
is a tight lattice if every proper tolerance 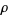 of
of 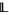 satisfies
satisfies
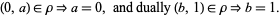 |
Tight lattices play an important role in the study of congruence lattices on finite algebras. One can show that a finite lattice 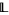 is tight if and only if it is
is tight if and only if it is 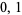 -simple and every strictly increasing meet endomorphism of
-simple and every strictly increasing meet endomorphism of 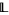 is constant. One can also show that a finite lattice
is constant. One can also show that a finite lattice 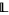 is tight if and only if its only connected tolerance is the all relation,
is tight if and only if its only connected tolerance is the all relation, 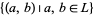 .
.
REFERENCES:
Grätzer, G. General Lattice Theory, 2nd ed. Boston, MA: Birkhäuser, 1998.
Hobby, D. and McKenzie, R. The Structure of Finite Algebras. Providence, RI: Amer. Math. Soc., 1988.
Insall, M. "Some Finiteness Conditions in Lattices Using Nonstandard Proof Methods." J. Austral. Math. Soc. 53, 266-280, 1992.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|