معادلات حركيات مفاعل عاري 

بالنظر إلى معادلة الاتية:

 نجد أننا سنعتبر هنا أن dn/dt لا تساوي صفراً، وحيث أننا سنهتم بتغير كثافة النيوترونات بالنسبة للزمن أو حيث أنه يوجد لدينا مجموعتين من النيوترونات الناتجة عن الانشطار وهما: النيوترونات اللحظية Prompt والنيوترونات المتأخرة Delayed فإنه علينا أن تأخذ هاتين المجموعتين الآن في الاعتبار. لنفترض أن نسبة النيوترونات المتأخرة في النيوترونات الانشطارية هي وبالتالي فإن عدد النيوترونات اللحظية هي (β ​- 1) ويكون معدل إنتاج هذه النيوترونات هو: K_∞ ∑_a ∅ (β ​- 1) أما معدل إنتاج النيوترونات المتأخرة فيمكن حسابة بمعرفة ثابت التحلل الإشعاعي (λ) لشظايا الانشطار التي تقوم بإطلاق هذه النيوترونات ومعدل تركيزاتها (C). وحيث أن لدينا ستة مجموعات من هذه النيوترونات المتأخرة فإن معدل إنتاج هذه النيوترونات الكلي (n_d (tot يعطي بالعلاقة :

(1)..............

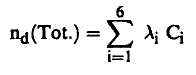
حيث λ_i, C_i تدل على النواة رقم (i).

وبالتالي فإن مصدر النيوترونات في المعادلة (1) يصبح مجموع النيوترونات المتأخرة واللحظية، أي أن:

(2)................

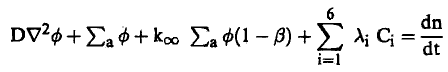
باستخدام علاقات سابقة، حيث نجد أن:

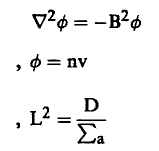
وبالتعويض في المعادلة السابقة نجد أن :

(3)..............

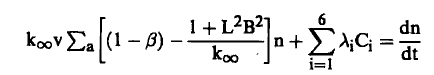
ولكن:

وبالتالي نجد أن:

(4)...............

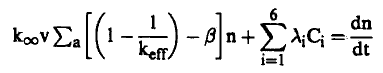
ومن معادلة الاتية:

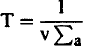
 نجد ان:

(5).............

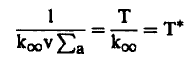
حيث *T زمن توليد النيوترون اللحظي Prompt Neutron Generation Time وبالتالي فإن معادلة (3) توضع على الصورة:

(6).................

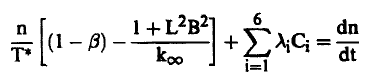
يمكن الآن تعريف المفاعلية: (Reactivity) للمفاعل (ρ) حيث:

(7) .................

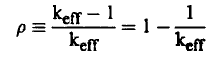
وبالتعويض في معادلة (6) وبعد قليل من الترتيبات، يمكن استنتاج أن :

(8)................

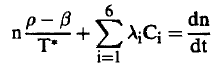
بقى أن نعرف الآن معدل تركيز الأنوية (_iC) أو معدل تكون النواة (i) الذي يعطى بالعلاقة:

(9)..............

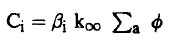
حيث و نسبة النيوترونات المتأخرة الناتجة عن النواة (أ) من النيوترونات الانشطارية التي معدل إنتاجها هو ∅ K_∞ ∑_a (كما بينا سابقا). وحسب قوانين النشاط الإشعاعي فإن معدل تكون النواة (i) المشعة للنيوترون dC_i/dt يعطي بالعلاقة:

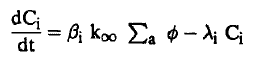
وحيث أن:nv = ∅ ومن معادلة (5) نجد أن العلاقة السابقة توضع على الصورة:

(10).........

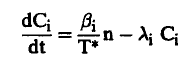
يحل معادلتي (8)، (10) يمكن دراسة حركية المفاعل.

لاحظ أن المفاعلية (ρ) تحدد أداء المفاعل حيث نجد أنه عندما:

المفاعل تحت حرج (يتوقف التفاعل)   ρ < 1    (1)

المفاعل في مرحلة الحروجة وهي     

مرحلة التشغيل المسيطر عليها.       (2)   ρ =0

المفاعل فوق حرج (التفاعل المتسلسل يتزايد باضطراد ولا بد من السيطرة عليه قبل حدوث كارثة الانفجار)       

                            (3) > 1    ρ 

إن معدل زيادة كثافة النيوترونات يحدده معدل الانشطار الذي يتناسب بدوره مع عدد النيوترونات (n) وبالتالي فإن حل معادلة (8) يمكن وضعه على الصورة:

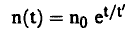
وكذلك، بالنسبة للمعادلة (10) فإن:

ولتوضيح الحالة التي نحن بصددها فإننا تعرف الآن الزمن الدوري للمفاعل (T_p) أو Reactor period: على أنه الزمن اللازم لتتغير كثافة النيوترونات بمعدل قدره e أي أن:

(11)........

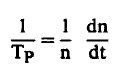
وبالتالي فأن:

(12)........

ويمكن استنتاج ان:

(13)..........

حيث (T_d) هي الزمن الدوري للمفاعل في حالة وجود النيترونات المتأخرة.

اما عند وجود نيوترونات لحظية فقط فأن الزمن الدوري للمفاعل T_p يعطي بالعلاقة:

(14)     ...........

لاحظ أنه عندما تكون المفاعلية (p) صغيرة جداً، فإن معادلة (13) تؤول إلى العلاقة:

(15)     ...........

يمكن الآن دراسة تأثير النيوترونات المتأخرة على الزمن الدوري للمفاعل وكيف تساعد على سهولة التحكم في المفاعل.

وبالتالي فإن التغير في المفاعلية يأخذ وقتاً قصيراً جداً في حالة وجود النيوترونات اللحظية فقط وبالتالي لا نستطيع تشغيل أية منظومة ميكانيكية للتحكم في المفاعل. أما عندما نعتبر وجود النيوترونات المتأخرة فإن الزمن الدوري للمفاعل يصبح 24 ثانية وهذه فترة زمنية كافية لشغيل قضبان التحكم والسيطرة على المفاعل ميكانيكياً.