Bernoulli's Method

In order to find a root of a polynomial equation

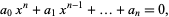(1)

consider the difference equation

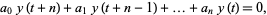(2)

which is known to have solution

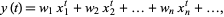(3)

where 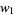, , 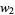..., are arbitrary functions of  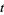with period 1, and 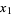, ...,  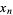are roots of (1). In order to find the absolutely greatest root (1), take any arbitrary values for 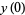, , 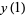..., 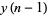. By repeated application of (2), calculate in succession the values 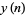, , 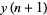, 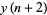.... Then the ratio of two successive members of this sequence tends in general to a limit, which is the absolutely greatest root of (1).

REFERENCES:

Whittaker, E. T. and Robinson, G. "A Method of Daniel Bernoulli." §52 in The Calculus of Observations: A Treatise on Numerical Mathematics, 4th ed. New York: Dover, pp. 98-99, 1967.