


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 15-10-2021
Date: 31-8-2021
Date: 26-8-2021
|
The conjugate gradient method can be applied on the normal equations. The CGNE and CGNR methods are variants of this approach that are the simplest methods for nonsymmetric or indefinite systems. Since other methods for such systems are in general rather more complicated than the conjugate gradient method, transforming the system to a symmetric definite one and then applying the conjugate gradient method is attractive for its coding simplicity.
CGNE solves the system
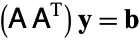 |
(1) |
for 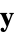 and then computes the solution
and then computes the solution
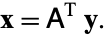 |
(2) |
CGNR solves
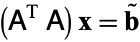 |
(3) |
for the solution vector 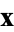 , where
, where
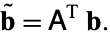 |
(4) |
If a system of linear equations 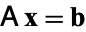 has a nonsymmetric, possibly indefinite (but nonsingular) coefficient matrix, one obvious attempt at a solution is to apply the conjugate gradient method to a related symmetric positive definite system
has a nonsymmetric, possibly indefinite (but nonsingular) coefficient matrix, one obvious attempt at a solution is to apply the conjugate gradient method to a related symmetric positive definite system 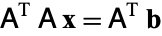 . While this approach is easy to understand and code, the convergence speed of the conjugate gradient method now depends on the square of the condition number of the original coefficient matrix. Thus the rate of convergence of the conjugate gradient procedure on the normal equations may be slow.
. While this approach is easy to understand and code, the convergence speed of the conjugate gradient method now depends on the square of the condition number of the original coefficient matrix. Thus the rate of convergence of the conjugate gradient procedure on the normal equations may be slow.
Several proposals have been made to improve the numerical stability of this method. The best known is by Paige and Saunders (1982) and is based upon applying the Lanczos method to the auxiliary system
![[I A; A^T 0][r; x]=[b; 0].](https://mathworld.wolfram.com/images/equations/ConjugateGradientMethodontheNormalEquations/NumberedEquation5.gif) |
(5) |
A clever execution of this scheme delivers the factors 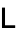 and
and 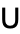 of the LU decomposition of the tridiagonal matrix that would have been computed by carrying out the Lanczos procedure with
of the LU decomposition of the tridiagonal matrix that would have been computed by carrying out the Lanczos procedure with 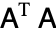 .
.
Another means for improving the numerical stability of this normal equations approach is suggested by Björck and Elfving (1979). The observation that the matrix 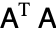 is used in the construction of the iteration coefficients through an inner product like
is used in the construction of the iteration coefficients through an inner product like 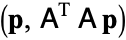 leads to the suggestion that such an inner product be replaced by
leads to the suggestion that such an inner product be replaced by 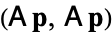 .
.
REFERENCES:
Barrett, R.; Berry, M.; Chan, T. F.; Demmel, J.; Donato, J.; Dongarra, J.; Eijkhout, V.; Pozo, R.; Romine, C.; and van der Vorst, H. Templates for the Solution of Linear Systems: Building Blocks for Iterative Methods, 2nd ed. Philadelphia, PA: SIAM, 1994. http://www.netlib.org/linalg/html_templates/Templates.html.
Björck, A. and Elfving, T. "Accelerated Projection Methods for Computing Pseudo-Inverse Solutions of Systems in Linear Equations." BIT 19, 145-163, 1979.
Paige, C. and Saunders, M. "LSQR: An Algorithm for Sparse Linear Equations and Sparse Least Squares." ACM Trans. Math. Soft. 8, 43-71, 1982.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|