المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Stirling,s Finite Difference Formula |
 1103
 06:52 مساءً
date: 29-11-2021 |
Author : Beyer, W. H. 
Book or Source : RC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press 
Page and Part : ...|
Read More
Date: 17-10-2021
2086
Date: 15-10-2021
1010
Date: 16-11-2021
983
|
 |
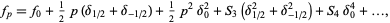(1) |
for ![p in [-1/2,1/2]](https://mathworld.wolfram.com/images/equations/StirlingsFiniteDifferenceFormula/Inline1.gif)
, where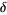 
is the central difference and
 |
 |
 |
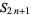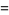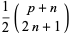(2) |
 |
 |
 |
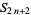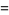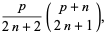(3) |
with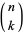 
a binomial coefficient.
REFERENCES:
Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 433, 1987.
Whittaker, E. T. and Robinson, G. "The Newton-Stirling Formula." §23 in The Calculus of Observations: A Treatise on Numerical Mathematics, 4th ed. New York: Dover, pp. 38-39, 1967.
|
|
|
|
"عادة ليلية" قد تكون المفتاح للوقاية من الخرف
|
|
|
|
|
|
|
ممتص الصدمات: طريقة عمله وأهميته وأبرز علامات تلفه
|
|
|
|
|
|
|
المجمع العلمي للقرآن الكريم يقيم جلسة حوارية لطلبة جامعة الكوفة
|
|
|
