ثابت الانحلال (λ): الطريقة الكمية

عند استخدام ميكانيكا الكم فإن موضع الجسيم يغدو غير ذي معنى. ونتحدث بدلاً من ذلك عن القيمة المتوقعة Expectation Value للموقع. وهذا يتفق مع مبدأ عدم التحديد (Δx. Δp ≃ h) وبالتالي يمكن تحديد احتمال ليجاد الجسيم أو القيمة المتوقعة لوجوده في عنصر الحجم (dx dy dz) إذا علمت دالة الموجة له (ψ). فإذا كان لدينا نظام يطلق إشعاع γ فإن دالة الموجة له تصبح دالة في الزمن. فإذا كان الانتقال يتم بين الحالة الابتدائية (i) إلى الحالة النهائية (f) كما بالشكل (1) فإن إحداثي الموضع x يجب أن يستبدل بعنصر مصفوفة الانتقال (Transition Matrix Element)

...............(1)

حيث ψ هي دالة الموجة الكلية (تعتمد على الزمن والموضع). وتعطى العلاقة:

 ومن ثم يمكن كتابة معادلة (1) على الصورة:

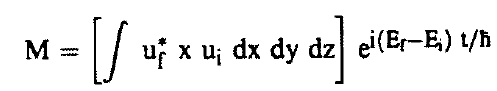........(2)

حيثE_i ، E_f هما طاقتي إثارة المستويين الابتدائي والنهائي (أنظر الشكل (1)).

u_i، u_f هما دالتي موجتي المستوين (الحالتين) الابتدائي والنهائي.

ويسمى الحد الأول في المعادلة السابقة بعنصر المصفوفةMatrix Element  المستقل عن الزمن ونرمز له بالرمز x_fi أي أن:

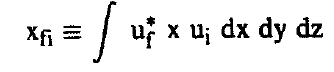
كما ويرمز له أحياناً بالصيغة:

   ..............(3)

وبالتالي يمكن كتابة احتمال الانتقال (λ) بدلالة عنصر المصفوفة على الصورة التالية:

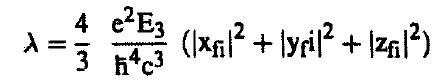...........(4)

حيث تمثل |z_fi| ,|x_fi|, |y_fi| عناصر المصفوفة لإحداثيات الموضع الثلاثة z ، y، x

E هي طاقة اشعة γ (أنظر الشكل 1).

الشكل (1) انتقال اشعة γ بين المستويين الابتدائي (i) والنهائي (f).