


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 1-12-2021
Date: 12-10-2021
Date: 23-9-2021
|
A problem also known as the points problem or unfinished game. Consider a tournament involving 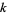 players playing the same game repetitively. Each game has a single winner, and denote the number of games won by player
players playing the same game repetitively. Each game has a single winner, and denote the number of games won by player 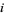 at some juncture
at some juncture 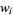 . The games are independent, and the probability of the
. The games are independent, and the probability of the 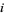 th player winning a game is
th player winning a game is 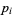 . The tournament is specified to continue until one player has won
. The tournament is specified to continue until one player has won 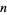 games. If the tournament is discontinued before any player has won
games. If the tournament is discontinued before any player has won 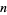 games so that
games so that 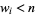 for
for 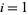 , ...,
, ..., 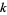 , how should the prize money be shared in order to distribute it proportionally to the players' chances of winning?
, how should the prize money be shared in order to distribute it proportionally to the players' chances of winning?
For player 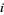 , call the number of games left to win
, call the number of games left to win 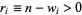 the "quota." For two players, let
the "quota." For two players, let 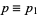 and
and 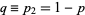 be the probabilities of winning a single game, and
be the probabilities of winning a single game, and 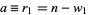 and
and 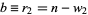 be the number of games needed for each player to win the tournament. Then the stakes should be divided in the ratio
be the number of games needed for each player to win the tournament. Then the stakes should be divided in the ratio 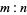 , where
, where
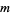 |
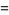 |
![p^a[1+a/1q+(a(a+1))/(2!)q^2+...+(a(a+1)...(a+b-2))/((b-1)!)q^(b-1)]](https://mathworld.wolfram.com/images/equations/SharingProblem/Inline20.gif) |
(1) |
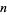 |
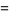 |
![q^b[1+b/1p+(b(b+1))/(2!)p^2+...+(b(b+1)...(b+a-2))/((a-1)!)p^(a-1)]](https://mathworld.wolfram.com/images/equations/SharingProblem/Inline23.gif) |
(2) |
(Kraitchik 1942).
If 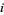 players have equal probability of winning ("cell probability"), then the chance of player
players have equal probability of winning ("cell probability"), then the chance of player 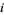 winning for quotas
winning for quotas 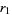 , ...,
, ..., 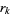 is
is
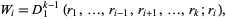 |
(3) |
where 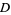 is the Dirichlet integral of type 2D. Similarly, the chance of player
is the Dirichlet integral of type 2D. Similarly, the chance of player 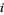 losing is
losing is
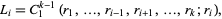 |
(4) |
where 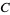 is the Dirichlet integral of type 2C. If the cell quotas are not equal, the general Dirichlet integral
is the Dirichlet integral of type 2C. If the cell quotas are not equal, the general Dirichlet integral 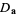 must be used, where
must be used, where
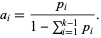 |
(5) |
If 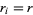 and
and 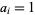 , then
, then 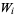 and
and 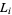 reduce to
reduce to 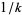 as they must. Let
as they must. Let 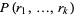 be the joint probability that the players would be statistically ranked in the order of the
be the joint probability that the players would be statistically ranked in the order of the 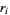 s in the argument list if the contest were completed. For
s in the argument list if the contest were completed. For 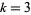 ,
,
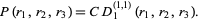 |
(6) |
For 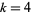 with quota vector
with quota vector 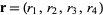 and
and 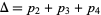 ,
,
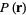 |
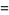 |
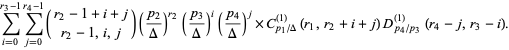 |
(7) |
An expression for 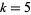 is given by Sobel and Frankowski (1994, p. 838).
is given by Sobel and Frankowski (1994, p. 838).
REFERENCES:
Kraitchik, M. "The Unfinished Game." §6.1 in Mathematical Recreations. New York: W. W. Norton, pp. 117-118, 1942.
Sobel, M. and Frankowski, K. "The 500th Anniversary of the Sharing Problem (The Oldest Problem in the Theory of Probability)." Amer. Math. Monthly 101, 833-847, 1994.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
بالصور: ممثل المرجعية العليا الشيخ عبد المهدي الكربلائي يؤم جموع المؤمنين في صلاة عيد الفطر المبارك داخل الصحن الحسيني الشريف
|
|
|