Hackenbush

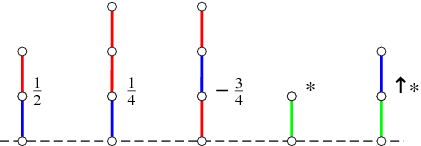
Hackenbush is a game in combinatorial game theory in which player Left can delete any bLue edge, player Right can delete any Red edge, and either player can delete Green edges. A hackenbush figure can be evaluated as a Conway game or surreal number. A few values are indicated above.

REFERENCES:

Berlekamp, E. R.; Conway, J. H.; and Guy, R. K. Winning Ways for Your Mathematical Plays. Wellesley, MA: A K Peters, 2004.

Conway, J. H. On Numbers and Games. Wellesley, MA: A K Peters, 2000.

Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, pp. 283-284, 1996.

Gonshor, H. An Introduction to Surreal Numbers. Cambridge, England: Cambridge University Press, 1986.

Knuth, D. Surreal Numbers: How Two Ex-Students Turned on to Pure Mathematics and Found Total Happiness. Reading, MA: Addison-Wesley, 1974. http://www-cs-faculty.stanford.edu/~knuth/sn.html.

Schleicher, D. and Stoll, M. "An Introduction to Conway's Numbers and Games." http://arxiv.org/abs/math.CO/0410026.

Sloane, N. J. A. Sequence A065401 in "The On-Line Encyclopedia of Integer Sequences."