


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 18-11-2021
Date: 15-2-2016
Date: 21-12-2021
|
In a game proposed by J. H. Conway, a devil chases an angel on an infinite chessboard. At each move, the devil can eliminate one of the squares, and the angel can make a leap in any direction, covering a distance of at most 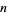 squares. Here,
squares. Here, 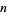 is a positive integer previously fixed, and is called the "power" of the angel. The devil's aim is to trap the angel on an island surrounded by a hole of width at least
is a positive integer previously fixed, and is called the "power" of the angel. The devil's aim is to trap the angel on an island surrounded by a hole of width at least 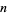 .
.
Can the angel indefinitely escape the devil, if his power is sufficiently high? Can the devil defeat an angel of any finite power? In 2006, Brian Bowditch proved that the 4-angel can win. Later that year, András Máthé proved the 2-angel will win, completely solving the problem.
REFERENCES:
Conway, J. "The Angel Problem." In Games of No Chance, Proc. MSRI Workshop on Combinatorial Games, July, 1994 (Ed. R. J. Nowakowski.) Cambridge, England: Cambridge University Press, pp. 3-12, 1996. http://www.msri.org/publications/books/Book29/files/conway.pdf.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
عقد جلسة حوارية عن ضحايا جرائم التطرف ضمن فعاليات اليوم الثاني لمؤتمر ذاكرة الألم
|
|
|