


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 21-8-2021
Date: 17-11-2021
Date: 19-9-2021
|

A ternary diagram is a triangular diagram which displays the proportion of three variables that sum to a constant and which does so using barycentric coordinates. The coordinate axes of such a diagram are shown in the figure above, where each of the x-, y-, and z-axes are scaled so that 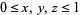 , and where the grid lines denote the values
, and where the grid lines denote the values 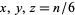 ,
, 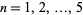 . In most instances, ternary plots are drawn on equilateral triangles as in the figure above, though it is not uncommon for certain scenarios to be better graphed on right triangular diagrams as well (West 2013).
. In most instances, ternary plots are drawn on equilateral triangles as in the figure above, though it is not uncommon for certain scenarios to be better graphed on right triangular diagrams as well (West 2013).
Ternary diagrams are sometimes called ternary plots, triangle plots, ternary graphs, simplex plots, and de Finetti diagrams, though the latter term is usually reserved for a specific family of ternary diagrams commonly studied in population genetics. Such diagrams are encountered often in the study of phase equilibria and appear somewhat often throughout a number of physical sciences.
| point | coordinates 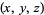 |
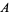 |
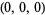 |
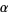 |
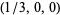 |
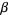 |
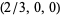 |
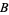 |
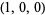 |
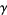 |
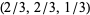 |
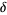 |
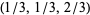 |
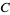 |
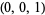 |
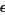 |
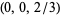 |
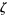 |
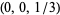 |
For convenience, there are a few "base points" plotted on the coordinate axes in the first figure. Among these are the barycenter 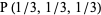 , as well as nine other points whose coordinates are given in the table above. Note that the points labeled
, as well as nine other points whose coordinates are given in the table above. Note that the points labeled 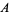 ,
, 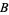 , and
, and 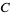 in the diagram refer to 100%
in the diagram refer to 100% 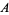 , 100%
, 100% 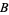 , and 100% C, respectively, as elaborated upon in the discussion that follows.
, and 100% C, respectively, as elaborated upon in the discussion that follows.

At first glance, it may appear as if the coordinates of points plotted on ternary graphs are chosen at random when, in fact, there are a number of equivalent ways to compute the ternary coordinates of a two-dimensional point 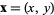 . The most visually intuitive way is to obtain them graphically, which can be done as illustrated in the figure above. First, draw the segments
. The most visually intuitive way is to obtain them graphically, which can be done as illustrated in the figure above. First, draw the segments 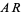 ,
, 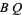 , and
, and 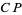 where here,
where here, 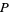 ,
, 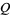 , and
, and 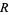 , respectively, are the points on the segments
, respectively, are the points on the segments 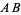 ,
, 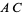 , and
, and 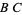 , respectively, that are the intersections of those segments with the rays through
, respectively, that are the intersections of those segments with the rays through  and beginning at
and beginning at 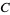 ,
, 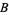 , and
, and 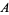 , respectively. Upon doing so, one gets the relations for the
, respectively. Upon doing so, one gets the relations for the 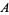 -,
-, 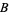 -, and
-, and 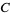 -coordinates--denoted
-coordinates--denoted 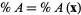 ,
, 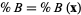 , and
, and 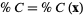 , respectively, to indicate that, in practice, these coordinates typically denote a weighted percentage of components
, respectively, to indicate that, in practice, these coordinates typically denote a weighted percentage of components 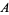 ,
, 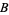 , and
, and 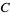 --by way of the relations
--by way of the relations
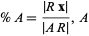 |
(1) |
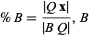 |
(2) |
and
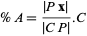 |
(3) |
Here, 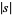 denotes the Euclidean length of a segment
denotes the Euclidean length of a segment 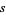 .
.
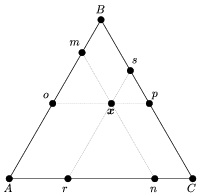
As shown in the figure above, a somewhat different geometric construction can be used to compute the ternary coordinates of a point 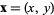 . Using this technique, one obtains the percentage of each component
. Using this technique, one obtains the percentage of each component 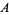 ,
, 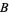 , and
, and 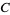 by drawing
by drawing 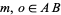 ,
, 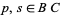 , and
, and 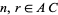 , and then by constructing segments
, and then by constructing segments 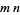 ,
, 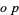 , and
, and 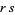 through
through  and parallel to sides
and parallel to sides 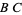 ,
, 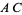 , and
, and 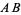 , respectively. In this case, the percentage of
, respectively. In this case, the percentage of 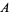 is equal to the length
is equal to the length 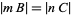 , while the percentage of
, while the percentage of 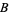 equals
equals 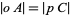 and the percentage of
and the percentage of 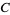 equals
equals 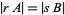 (West 2013). Using this method, it is often beneficial to draw triangular grid lines as in the first figure above.
(West 2013). Using this method, it is often beneficial to draw triangular grid lines as in the first figure above.
A less-visual, more algebraic way to compute the ternary coordinates of a point  is to first consider the stereographic projection of the triple
is to first consider the stereographic projection of the triple 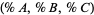 as a point on the standard 2-simplex in
as a point on the standard 2-simplex in 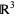 . Using this method, one identifies 100% of components
. Using this method, one identifies 100% of components 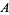 ,
, 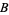 , and
, and 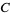 , respectively, with the coordinates
, respectively, with the coordinates 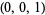 ,
, 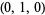 , and
, and 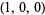 , respectively, and performs a natural stereographic projection from
, respectively, and performs a natural stereographic projection from 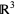 to
to 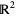 by isometrically rotating the three coordinate axes. Doing so yields what appears to be an equilateral triangle in
by isometrically rotating the three coordinate axes. Doing so yields what appears to be an equilateral triangle in 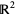 with 100%
with 100% 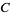 at
at 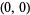 , 100%
, 100% 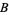 at
at 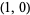 , and 100%
, and 100% 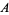 at
at
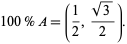 |
(4) |
The result is that the Cartesian ternary coordinates assigned to an arbitrary triple 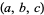 ,
, 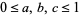 , have the form
, have the form
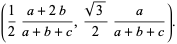 |
(5) |
The representation of data as a ternary diagram has some benefit. In addition to the obvious benefit of presenting three-variable data in a two-dimensional plot, the use of the triangular axes can serve to quickly represent certain phenomena. For example, in the first figure, the grid lines parallel to, e.g., segment 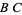 represent the points for which %
represent the points for which %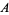 is constant. Similarly, in the second figure, segments including either
is constant. Similarly, in the second figure, segments including either 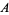 ,
, 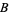 , or
, or 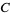 represent data for which the ratio of the of the other two components is constant; for example, the ratio
represent data for which the ratio of the of the other two components is constant; for example, the ratio 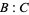 is fixed along segment
is fixed along segment 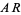 in the second figure (Cornish).
in the second figure (Cornish).
REFERENCES:
Bogomolny, A. "Barycentric Coordinates, Three Jugs Application." Interactive Mathematics Miscellany and Puzzles. http://www.cut-the-knot.org/triangle/glasses.shtml.
Cornish, L. "Ternary Phase Diagrams." http://sig.ias.edu/files/Ternary%20Phase%20Diagrams.pdf.
Vaughn, W. "Ternary Plots." 2010. http://wvaughan.org/ternaryplots.html.
West, D. Ternary Equilibrium Diagrams, 2nd ed. New York: Springer, 2013.



|
|
|
|
"عادة ليلية" قد تكون المفتاح للوقاية من الخرف
|
|
|
|
|
|
|
ممتص الصدمات: طريقة عمله وأهميته وأبرز علامات تلفه
|
|
|
|
|
|
|
الأمين العام للعتبة العسكرية المقدسة يستقبل شيوخ ووجهاء عشيرة البو بدري في مدينة سامراء
|
|
|