


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 19-12-2021
Date: 2-10-2021
Date: 6-1-2016
|
The Jordan canonical form, also called the classical canonical form, of a special type of block matrix in which each block consists of Jordan blocks with possibly differing constants  . In particular, it is a block matrix of the form
. In particular, it is a block matrix of the form
![[lambda_1 1 0 ... 0; 0 lambda_1 1 ... 0; 0 0 lambda_1 ... 0; | ... ... ... 1; 0 0 0 ... lambda_1 ; ... ; lambda_k 1 0 ... 0; 0 lambda_k 1 ... 0; 0 0 lambda_k ... 0; | ... ... ... 1; 0 0 0 ... lambda_k]](https://mathworld.wolfram.com/images/equations/JordanCanonicalForm/NumberedEquation1.gif) |
(1) |
(Ayres 1962, p. 206).
A specific example is given by
![[5 1 0 0 0 0; 0 5 1 0 0 0; 0 0 5 0 0 0; 0 0 0 1-2i 1 0; 0 0 0 0 1-2i 1; 0 0 0 0 0 1-2i],](https://mathworld.wolfram.com/images/equations/JordanCanonicalForm/NumberedEquation2.gif) |
(2) |
which has three Jordan blocks. (Note that the degenerate case of a  matrix is considered a Jordan block even though it lacks a superdiagonal to be filled with 1s; cf. Strang 1988, p. 454).
matrix is considered a Jordan block even though it lacks a superdiagonal to be filled with 1s; cf. Strang 1988, p. 454).
Any complex matrix 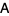 can be written in Jordan canonical form by finding a Jordan basis
can be written in Jordan canonical form by finding a Jordan basis  for each Jordan block. In fact, any matrix with coefficients in an algebraically closed field can be put into Jordan canonical form. The dimensions of the blocks corresponding to the eigenvalue
for each Jordan block. In fact, any matrix with coefficients in an algebraically closed field can be put into Jordan canonical form. The dimensions of the blocks corresponding to the eigenvalue 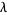 can be recovered by the sequence
can be recovered by the sequence
 |
(3) |
The convention that the submatrices have 1s on the subdiagonal instead of the superdiagonal is also used sometimes (Faddeeva 1958, p. 50).
REFERENCES:
Ayres, F. Jr. Schaum's Outline of Theory and Problems of Matrices. New York: Schaum, 1962.
Faddeeva, V. N. Computational Methods of Linear Algebra. New York: Dover, p. 50, 1958.
Strang, G. Linear Algebra and its Applications, 3rd ed. Philadelphia, PA: Saunders, 1988.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|