


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 1-9-2021
Date: 6-1-2016
Date: 18-10-2021
|
 |
 |
 |
The Menger sponge is a fractal which is the three-dimensional analog of the Sierpiński carpet.
The 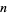 th iteration of the Menger sponge is implemented in the Wolfram Language as MengerMesh[n, 3].
th iteration of the Menger sponge is implemented in the Wolfram Language as MengerMesh[n, 3].
Let 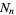 be the number of filled boxes,
be the number of filled boxes, 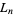 the length of a side of a hole, and
the length of a side of a hole, and 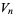 the fractional volume after the
the fractional volume after the  th iteration, then
th iteration, then
 |
 |
 |
(1) |
 |
 |
 |
(2) |
 |
 |
 |
(3) |
The capacity dimension is therefore
 |
 |
 |
(4) |
 |
 |
 |
(5) |
 |
 |
 |
(6) |
 |
 |
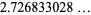 |
(7) |
(OEIS A102447).
The Menger sponge, in addition to being a fractal, is also a super-object for all compact one-dimensional objects, i.e., the topological equivalent of all one-dimensional objects can be found in a Menger sponge (Peitgen et al. 1992).

The image above shows a metal print of the Menger sponge created by digital sculptor Bathsheba Grossman (http://www.bathsheba.com/).
REFERENCES:
Dickau, R. "Sierpinski-Menger Sponge Code and Graphic." http://library.wolfram.com/infocenter/MathSource/4662/.
Dickau, R. M. "Menger (Sierpinski) Sponge." http://mathforum.org/advanced/robertd/sponge.html.
Gleick, J. Chaos: Making a New Science. New York: Penguin Books, p. 101, 1988.
Grossman, B. "Menger Sponge." http://www.bathsheba.com/math/menger.
Kosmulski, M. "Modulus Origami--Fractals, IFS." http://hektor.umcs.lublin.pl/~mikosmul/origami/fractals.html.
Mandelbrot, B. B. The Fractal Geometry of Nature. New York: W. H. Freeman, p. 145, 1983.
Mosely, J. "Menger's Sponge (Depth 3)." http://world.std.com/~j9/sponge/.
Peitgen, H.-O.; Jürgens, H.; and Saupe, D. Chaos and Fractals: New Frontiers of Science. New York: Springer-Verlag, 1992.
Sloane, N. J. A. Sequence A102447 in "The On-Line Encyclopedia of Integer Sequences."
Werbeck, S. "A Journey into Menger's Sponge." http://www.angelfire.com/art2/stw/.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
العتبة العباسية المقدسة تستعد لإطلاق الحفل المركزي لتخرج طلبة الجامعات العراقية
|
|
|