


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 28-9-2021
Date: 6-10-2021
Date: 31-8-2021
|

The Cantor set 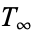 , sometimes also called the Cantor comb or no middle third set (Cullen 1968, pp. 78-81), is given by taking the interval
, sometimes also called the Cantor comb or no middle third set (Cullen 1968, pp. 78-81), is given by taking the interval ![[0,1]](https://mathworld.wolfram.com/images/equations/CantorSet/Inline2.gif) (set
(set 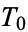 ), removing the open middle third (
), removing the open middle third (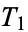 ), removing the middle third of each of the two remaining pieces (
), removing the middle third of each of the two remaining pieces (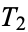 ), and continuing this procedure ad infinitum. It is therefore the set of points in the interval
), and continuing this procedure ad infinitum. It is therefore the set of points in the interval ![[0,1]](https://mathworld.wolfram.com/images/equations/CantorSet/Inline6.gif) whose ternary expansions do not contain 1, illustrated above.
whose ternary expansions do not contain 1, illustrated above.
The 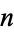 th iteration of the Cantor is implemented in the Wolfram Language as CantorMesh[n].
th iteration of the Cantor is implemented in the Wolfram Language as CantorMesh[n].
Iterating the process 1 -> 101, 0 -> 000 starting with 1 gives the sequence 1, 101, 101000101, 101000101000000000101000101, .... The sequence of binary bits thus produced is therefore 1, 0, 1, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0, ... (OEIS A088917) whose 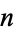 th term is amazingly given by
th term is amazingly given by 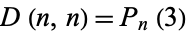 (mod 3), where
(mod 3), where 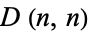 is a (central) Delannoy number and
is a (central) Delannoy number and 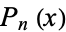 is a Legendre polynomial (E. W. Weisstein, Apr. 9, 2006). The recurrence plot for this sequence is illustrated above.
is a Legendre polynomial (E. W. Weisstein, Apr. 9, 2006). The recurrence plot for this sequence is illustrated above.
This produces the set of real numbers 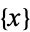 such that
such that
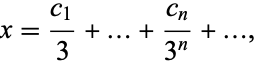 |
(1) |
where 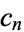 may equal 0 or 2 for each
may equal 0 or 2 for each 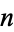 . This is an infinite, perfect set. The total length of the line segments in the
. This is an infinite, perfect set. The total length of the line segments in the 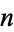 th iteration is
th iteration is
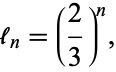 |
(2) |
and the number of line segments is 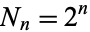 , so the length of each element is
, so the length of each element is
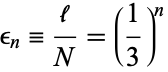 |
(3) |
and the capacity dimension is
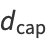 |
 |
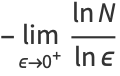 |
(4) |
 |
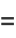 |
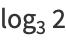 |
(5) |
 |
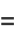 |
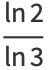 |
(6) |
 |
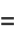 |
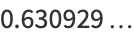 |
(7) |
(OEIS A102525). The Cantor set is nowhere dense, and has Lebesgue measure 0.
A general Cantor set is a closed set consisting entirely of boundary points. Such sets are uncountable and may have 0 or positive Lebesgue measure. The Cantor set is the only totally disconnected, perfect, compact metric space up to a homeomorphism (Willard 1970).
REFERENCES:
Boas, R. P. Jr. A Primer of Real Functions. Washington, DC: Amer. Math. Soc., 1996.
Cullen, H. F. Introduction to General Topology. Boston, MA: Heath, pp. 78-81, 1968.
Gleick, J. Chaos: Making a New Science. New York: Penguin Books, p. 93, 1988.
Lauwerier, H. Fractals: Endlessly Repeated Geometric Figures. Princeton, NJ: Princeton University Press, pp. 15-20, 1991.
Harris, J. W. and Stocker, H. "Cantor Set." §4.11.4 in Handbook of Mathematics and Computational Science. New York: Springer-Verlag, p. 114, 1998.
Sloane, N. J. A. Sequence A102525 in "The On-Line Encyclopedia of Integer Sequences."
Trott, M. The Mathematica GuideBook for Graphics. New York: Springer-Verlag, pp. 9-13, 2004. http://www.mathematicaguidebooks.org/.
Willard, S. §30.4 in General Topology. Reading, MA: Addison-Wesley, 1970.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|