


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 25-11-2021
Date: 24-11-2021
Date: 17-11-2021
|
There are several versions of the Kaplan-Yorke conjecture, with many of the higher dimensional ones remaining unsettled. The original Kaplan-Yorke conjecture (Kaplan and Yorke 1979) proposed that, for a two-dimensional mapping, the capacity dimension 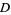 equals the Kaplan-Yorke dimension
equals the Kaplan-Yorke dimension 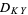 ,
,
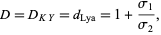 |
where 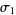 and
and 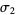 are the Lyapunov characteristic exponents. This was subsequently proven to be true in 1982. A later conjecture held that the Kaplan-Yorke dimension is generically equal to a probabilistic dimension which appears to be identical to the information dimension (Frederickson et al. 1983). This conjecture is partially verified by Ledrappier (1981). For invertible two-dimensional maps,
are the Lyapunov characteristic exponents. This was subsequently proven to be true in 1982. A later conjecture held that the Kaplan-Yorke dimension is generically equal to a probabilistic dimension which appears to be identical to the information dimension (Frederickson et al. 1983). This conjecture is partially verified by Ledrappier (1981). For invertible two-dimensional maps, 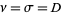 , where
, where  is the correlation exponent,
is the correlation exponent, 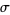 is the information dimension, and
is the information dimension, and 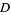 is the capacity dimension (Young 1984).
is the capacity dimension (Young 1984).
REFERENCES:
Chen, Z. M. "A Note on Kaplan-Yorke-Type Estimates on the Fractal Dimension of Chaotic Attractors." Chaos, Solitons, and Fractals 3, 575-582, 1994.
Frederickson, P.; Kaplan, J. L.; Yorke, E. D.; and Yorke, J. A. "The Liapunov Dimension of Strange Attractors." J. Diff. Eq. 49, 185-207, 1983.
Kaplan, J. L. and Yorke, J. A. In Functional Differential Equations and Approximations of Fixed Points: Proceedings, Bonn, July 1978 (Ed. H.-O. Peitgen and H.-O. Walther). Berlin: Springer-Verlag, p. 204, 1979.
Ledrappier, F. "Some Relations Between Dimension and Lyapunov Exponents." Commun. Math. Phys. 81, 229-238, 1981.
Worzbusekros, A. "Remark on a Conjecture of Kaplan and Yorke." Proc. Amer. Math. Soc. 85, 381-382, 1982.
Young, L. S. "Dimension, Entropy, and Lyapunov Exponents in Differentiable Dynamical Systems." Phys. A 124, 639-645, 1984.



|
|
|
|
مخاطر خفية لمكون شائع في مشروبات الطاقة والمكملات الغذائية
|
|
|
|
|
|
|
"آبل" تشغّل نظامها الجديد للذكاء الاصطناعي على أجهزتها
|
|
|
|
|
|
|
تستخدم لأول مرة... مستشفى الإمام زين العابدين (ع) التابع للعتبة الحسينية يعتمد تقنيات حديثة في تثبيت الكسور المعقدة
|
|
|