


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 16-11-2021
Date: 29-8-2021
Date: 23-9-2021
|
Consider the circle map. If 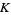 is nonzero, then the motion is periodic in some finite region surrounding each rational
is nonzero, then the motion is periodic in some finite region surrounding each rational 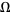 . This execution of periodic motion in response to an irrational forcing is known as mode locking. If a plot is made of
. This execution of periodic motion in response to an irrational forcing is known as mode locking. If a plot is made of 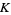 versus
versus 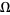 with the regions of periodic mode-locked parameter space plotted around rational
with the regions of periodic mode-locked parameter space plotted around rational 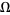 values (the map winding numbers), then the regions are seen to widen upward from 0 at
values (the map winding numbers), then the regions are seen to widen upward from 0 at 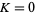 to some finite width at
to some finite width at 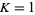 . The region surrounding each rational number is known as an Arnold tongue.
. The region surrounding each rational number is known as an Arnold tongue.
At 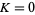 , the Arnold tongues are an isolated set of measure zero. At
, the Arnold tongues are an isolated set of measure zero. At 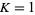 , they form a general cantor set of dimension
, they form a general cantor set of dimension 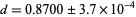 (Rasband 1990, p. 131). In general, an Arnold tongue is defined as a resonance zone emanating out from rational numbers in a two-dimensional parameter space of variables.
(Rasband 1990, p. 131). In general, an Arnold tongue is defined as a resonance zone emanating out from rational numbers in a two-dimensional parameter space of variables.
REFERENCES:
Rasband, S. N. Chaotic Dynamics of Nonlinear Systems. New York: Wiley, pp. 130-131, 1990.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|