Product Topology

The topology on the Cartesian product 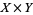 of two topological spaces whose open sets are the unions of subsets 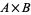, where  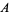and 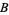 are open subsets of  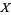and 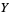, respectively.

This definition extends in a natural way to the Cartesian product of any finite number 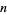 of topological spaces. The product topology of

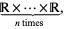where 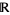 is the real line with the Euclidean topology, coincides with the Euclidean topology of the Euclidean space .

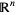In the definition of product topology of 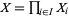, where  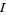is any set, the open sets are the unions of subsets 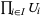, where  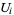is an open subset of  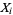with the additional condition that  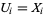for all but finitely many indices  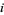(this is automatically fulfilled if  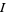is a finite set). The reason for this choice of open sets is that these are the least needed to make the projection onto the 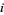th factor  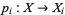continuous for all indices 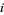. Admitting all products of open sets would give rise to a larger topology (strictly larger if  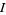is infinite), called the box topology.

The product topology is also called Tychonoff topology, but this should not cause any confusion with the notion of Tychonoff space, which has a completely different meaning.

REFERENCES:

Cullen, H. F. Introduction to General Topology. Boston, MA: Heath, pp. 65-91, 1968.

Joshi, K. D. "Product Topology." §8.2 in Introduction to General Topology. New Delhi, India: Wiley, pp. 196-203, 1983.

McCarty, G. "Tychonoff for Two." In Topology, an Introduction with Application to Topological Groups. New York: McGraw-Hill, pp. 154-157, 1967.

Willard, S. "Product Spaces, Weak Topologies." §8 in General Topology. Reading, MA: Addison-Wesley, pp. 52-59, 1970.