


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 2-8-2021
Date: 2-8-2021
Date: 28-7-2021
|
A hyper-Kähler manifold can be defined as a Riemannian manifold of dimension 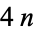 with three covariantly constant orthogonal automorphisms
with three covariantly constant orthogonal automorphisms 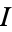 ,
, 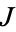 ,
, 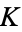 of the tangent bundle which satisfy the quaternionic identities
of the tangent bundle which satisfy the quaternionic identities
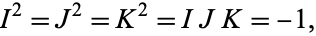 |
(1) |
where 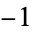 denotes the negative of the identity automorphism
denotes the negative of the identity automorphism 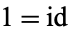 on the tangent bundle. The term hyper-Kähler is sometimes written without a hyphen (as hyperKähler) or without capitalization (as hyperkähler).
on the tangent bundle. The term hyper-Kähler is sometimes written without a hyphen (as hyperKähler) or without capitalization (as hyperkähler).
This definition is equivalent to several others commonly encountered in the literature; indeed, a manifold 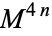 is said to be hyper-Kähler if and only if:
is said to be hyper-Kähler if and only if:
1. 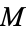 is a holomorphically symplectic Kähler manifold with holonomy in
is a holomorphically symplectic Kähler manifold with holonomy in 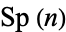 .
.
2. 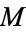 is a holomorphically symplectic Kähler manifold which is Ricci-flat (i.e., which has zero scalar curvature.
is a holomorphically symplectic Kähler manifold which is Ricci-flat (i.e., which has zero scalar curvature.
The first of the above equivalences is referring to Berger's classification of the holonomy groups of Riemannian manifolds and implies that parallel transport preserves 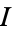 ,
, 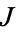 , and
, and 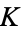 . Both this criterion and the criterion listed in the second of the above equivalences is used to differentiate hyperkähler manifolds from the similarly-named quaternionic-Kähler manifolds which have nonzero Ricci curvature and, in general, fail to be Kähler.
. Both this criterion and the criterion listed in the second of the above equivalences is used to differentiate hyperkähler manifolds from the similarly-named quaternionic-Kähler manifolds which have nonzero Ricci curvature and, in general, fail to be Kähler.
Hyper-kähler manifolds are necessarily Calabi-Yau manifolds and are Einstein manifolds with constant 0.
Generally, the automorphisms 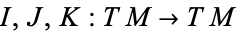 are assumed to be integrable. The presence of these three complex structures induces three Kähler 2-forms
are assumed to be integrable. The presence of these three complex structures induces three Kähler 2-forms 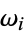 ,
, 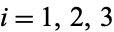 , on
, on 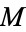 , namely
, namely
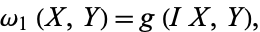 |
(2) |
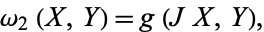 |
(3) |
and
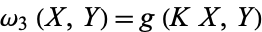 |
(4) |
for all 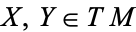 where, here,
where, here, 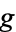 is the Kähler/Riemannian metric on
is the Kähler/Riemannian metric on 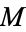 . As the two equivalent definitions above indicate, hyperkähler manifolds are holomorphically symplectic, i.e., they have three holomorphic symplectic 2-forms induced by each of
. As the two equivalent definitions above indicate, hyperkähler manifolds are holomorphically symplectic, i.e., they have three holomorphic symplectic 2-forms induced by each of 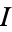 ,
, 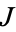 , and
, and 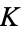 . For example, the 2-form
. For example, the 2-form 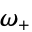 of the form
of the form
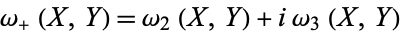 |
(5) |
is holomorphic and symplectic on 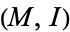 (where
(where 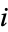 denotes the standard imaginary unit). Calabi proved a partial converse which says that a compact holomorphically symplectic Kähler manifold admits a unique hyper-Kähler metric with respect to any of its Kähler forms.
denotes the standard imaginary unit). Calabi proved a partial converse which says that a compact holomorphically symplectic Kähler manifold admits a unique hyper-Kähler metric with respect to any of its Kähler forms.
All even-dimensional complex vector spaces and tori are hyper-Kähler. Further examples include the quaternions 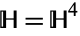 , the cotangent bundle
, the cotangent bundle 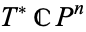 of
of 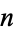 -dimensional complex projective space, K3 surfaces, Hilbert schemes of points on compact hyper-kähler 4-manifolds, and generalized Kummer varieties, as well as various moduli spaces, spaces of solutions to Nahm's equations, and the Nakajima quiver varieties.
-dimensional complex projective space, K3 surfaces, Hilbert schemes of points on compact hyper-kähler 4-manifolds, and generalized Kummer varieties, as well as various moduli spaces, spaces of solutions to Nahm's equations, and the Nakajima quiver varieties.



|
|
|
|
مخاطر خفية لمكون شائع في مشروبات الطاقة والمكملات الغذائية
|
|
|
|
|
|
|
"آبل" تشغّل نظامها الجديد للذكاء الاصطناعي على أجهزتها
|
|
|
|
|
|
|
المجمع العلميّ يُواصل عقد جلسات تعليميّة في فنون الإقراء لطلبة العلوم الدينيّة في النجف الأشرف
|
|
|