


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 9-8-2021
Date: 18-7-2021
Date: 22-6-2021
|
The Grassmannian 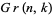 is the set of
is the set of 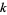 -dimensional subspaces in an
-dimensional subspaces in an 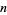 -dimensional vector space. For example, the set of lines
-dimensional vector space. For example, the set of lines 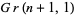 is projective space. The real Grassmannian (as well as the complex Grassmannian) are examples of manifolds. For example, the subspace
is projective space. The real Grassmannian (as well as the complex Grassmannian) are examples of manifolds. For example, the subspace 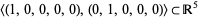 has a neighborhood
has a neighborhood 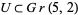 . A subspace
. A subspace 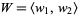 is in
is in 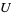 if
if 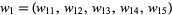 and
and 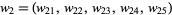 and
and 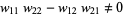 . Then for any
. Then for any 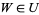 , the vectors
, the vectors 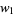 and
and 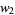 are uniquely determined by requiring
are uniquely determined by requiring 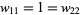 and
and 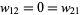 . The other six entries provide coordinates for
. The other six entries provide coordinates for 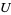 .
.
In general, the Grassmannian can be given coordinates in a similar way at a point 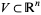 . Let
. Let 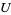 be the open set of
be the open set of 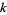 -dimensional subspaces which project onto
-dimensional subspaces which project onto 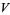 . First one picks an orthonormal basis
. First one picks an orthonormal basis 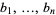 for
for 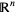 such that
such that 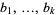 span
span 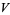 . Using this basis, it is possible to take any
. Using this basis, it is possible to take any 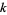 vectors and make a
vectors and make a 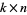 matrix. Doing this for the basis of
matrix. Doing this for the basis of 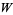 , another
, another 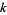 -dimensional subspace in
-dimensional subspace in 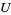 , gives a
, gives a 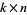 -matrix, which is well-defined up to linear combinations of the rows. The final step is to row-reduce so that the first
-matrix, which is well-defined up to linear combinations of the rows. The final step is to row-reduce so that the first 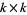 block is the identity matrix. Then the last
block is the identity matrix. Then the last 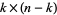 block is uniquely determined by
block is uniquely determined by 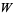 . The entries in this block give coordinates for the open set
. The entries in this block give coordinates for the open set 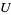 .
.
If 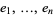 is the standard basis of
is the standard basis of 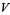 , a basis of
, a basis of 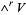 is given by the
is given by the 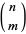 vectors
vectors 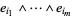 ,
, 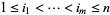 . If
. If 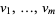 is a basis of a subspace
is a basis of a subspace  of dimension
of dimension  of
of 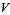 ,
, 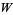 corresponds to a point
corresponds to a point 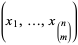 of
of 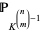 , whose coordinates are the components of
, whose coordinates are the components of 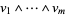 with respect to the basis of
with respect to the basis of 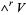 given above. These coordinates are the so-called Grassmann coordinates of
given above. These coordinates are the so-called Grassmann coordinates of 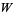 .
.
A different choice of the basis of 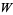 yields a different
yields a different 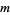 -tuple of coordinates, which differs from the original
-tuple of coordinates, which differs from the original 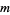 -tuple by a nonzero multiplicative constant, hence it corresponds to the same point.
-tuple by a nonzero multiplicative constant, hence it corresponds to the same point.
The Grassmannian is also a homogeneous space. A subspace is determined by its basis vectors. The group that permutes basis vectors is 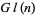 . The matrix that fixes
. The matrix that fixes 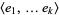 is a diagonal block matrix, with a
is a diagonal block matrix, with a 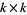 nonsingular matrix in the top left, and a
nonsingular matrix in the top left, and a 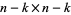 invertible matrix in the lower right.
invertible matrix in the lower right. 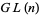 acts transitively on the Grassmannian
acts transitively on the Grassmannian 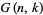 . Let
. Let 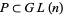 be the stabilizer (or isotropy) of
be the stabilizer (or isotropy) of 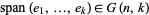 . Then
. Then 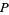 is the subgroup of
is the subgroup of 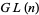 consisting of matrices
consisting of matrices ![A=[a_(i,j)]](https://mathworld.wolfram.com/images/equations/Grassmannian/Inline65.gif) such that
such that 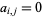 for all
for all 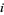 ,
, 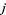 such that
such that 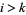 and
and 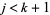 .
. 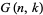 is isomorphic to
is isomorphic to 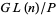 .
.
The tangent space to the Grassmannian is given by 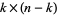 matrices, i.e., linear maps from
matrices, i.e., linear maps from 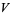 to the quotient vector space
to the quotient vector space 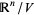 .
.
The elements 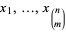 are the
are the 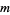 -minors of the
-minors of the 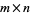 matrix whose
matrix whose 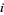 th row contains the components of
th row contains the components of 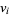 with respect to the basis
with respect to the basis 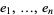 . It corresponds to a linear transformation
. It corresponds to a linear transformation 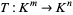 whose range is
whose range is 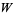 . In general, the range of such a linear transformation has dimension
. In general, the range of such a linear transformation has dimension 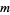 iff the corresponding
iff the corresponding 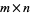 matrix has rank
matrix has rank  .
.
Let 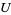 be the subset of
be the subset of 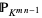 defined by the condition that all the
defined by the condition that all the 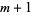 -minors of the matrix
-minors of the matrix 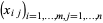 (which can be viewed as a sequence of
(which can be viewed as a sequence of 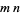 coordinates) be equal to zero, and one
coordinates) be equal to zero, and one 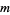 -minor be nonzero. The Grassmannian
-minor be nonzero. The Grassmannian 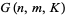 can be viewed as the image of the map
can be viewed as the image of the map 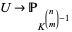 which maps each matrix of
which maps each matrix of 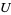 to the sequence of its
to the sequence of its 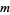 -minors.
-minors.
It as an algebraic projective algebraic variety defined by equations called Plücker's equations. It is a nonsingular variety of dimension 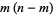 .
.
REFERENCES:
Fulton, W. Schubert Varieties and Degeneracy Loci. New York: Springer-Verlag, 1998.
Harris, J. "Grassmannians and Related Varieties." Lecture 6 in Algebraic Geometry: A First Course. New York: Springer-Verlag, pp. 63-71, 1992.
Kleiman, S. and Laksov, D. "Schubert Calculus." Amer. Math. Monthly 79, 1061-1082, 1972.
Shafarevich, I. R. Basic Algebraic Geometry, Vol. 1, 2nd ed. Berlin: Springer-Verlag, pp. 42-44, 1994.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
العتبة العباسية المقدسة تقدم دعوة إلى كلية مزايا الجامعة للمشاركة في حفل التخرج المركزي الخامس
|
|
|