


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 20-5-2021
Date: 23-7-2021
Date: 10-6-2021
|
A braid index is the least number of strings needed to make a closed braid representation of a link. The braid index is equal to the least number of Seifert circles in any projection of a knot (Yamada 1987). Also, for a nonsplittable link with link crossing number 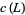 and braid index
and braid index 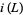 ,
,
![c(L)>=2[i(L)-1]](https://mathworld.wolfram.com/images/equations/BraidIndex/NumberedEquation1.gif) |
(Ohyama 1993). Let 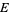 be the largest and
be the largest and 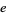 the smallest power of
the smallest power of 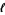 in the HOMFLY polynomial of an oriented link, and
in the HOMFLY polynomial of an oriented link, and 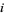 be the braid index. Then the morton-franks-williams inequality holds,
be the braid index. Then the morton-franks-williams inequality holds,
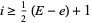 |
(Franks and Williams 1987). The inequality is sharp for all prime knots up to 10 crossings with the exceptions of 09-042, 09-049, 10-132, 10-150, and 10-156.
REFERENCES:
Franks, J. and Williams, R. F. "Braids and the Jones Polynomial." Trans. Amer. Math. Soc. 303, 97-108, 1987.
Jones, V. F. R. "Hecke Algebra Representations of Braid Groups and Link Polynomials." Ann. Math. 126, 335-388, 1987.
Ohyama, Y. "On the Minimal Crossing Number and the Brad Index of Links." Canad. J. Math. 45, 117-131, 1993.
Yamada, S. "The Minimal Number of Seifert Circles Equals the Braid Index of a Link." Invent. Math. 89, 347-356, 1987.



|
|
|
|
"عادة ليلية" قد تكون المفتاح للوقاية من الخرف
|
|
|
|
|
|
|
ممتص الصدمات: طريقة عمله وأهميته وأبرز علامات تلفه
|
|
|
|
|
|
|
المجمع العلمي للقرآن الكريم يقيم جلسة حوارية لطلبة جامعة الكوفة
|
|
|