


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 29-6-2021
Date: 5-8-2021
Date: 17-6-2021
|
A transition function describes the difference in the way an object is described in two separate, overlapping coordinate charts, where the description of the same set may change in different coordinates. This even occurs in Euclidean space 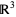 , where any rotation of the usual
, where any rotation of the usual  ,
, 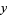 , and
, and 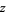 axes gives another set of coordinates.
axes gives another set of coordinates.
For example, on the sphere, person 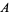 at the equator can use the usual directions of north, south, east, and west, but person
at the equator can use the usual directions of north, south, east, and west, but person 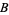 at the north pole must use something else. However, both
at the north pole must use something else. However, both 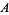 and
and 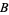 can describe the region in between them in their coordinate charts. A transition function would then describe how to go from the coordinate chart for
can describe the region in between them in their coordinate charts. A transition function would then describe how to go from the coordinate chart for 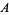 to the coordinate chart for
to the coordinate chart for 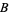 .
.
In the case of a manifold, a transition function is a map from one coordinate chart to another. Therefore, in a sense, a manifold is composed of coordinate charts, and the glue that holds them together is the transition functions. In the case of a bundle, the transition functions are the glue that holds together its trivializations. Specifically, in this case the transition function describes an invertible transformation of the fiber.
Naturally, the type of invertible transformation depends on the type of bundle. For instance, a vector bundle, which could be the tangent bundle, has invertible linear transition functions. More precisely, a transition function for a vector bundle of bundle rank 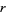 , on overlapping coordinate charts
, on overlapping coordinate charts 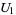 and
and 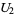 , is given by a function
, is given by a function
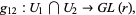 |
where 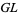 is the general linear group. The fiber at
is the general linear group. The fiber at 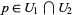 has two descriptions, and
has two descriptions, and 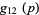 is the invertible linear map that takes one to the other. The transition functions have to be consistent in the sense that if one goes to another description of the same set, and then back again, then nothing has changed. A necessary and sufficient condition for consistency is the following: Given three overlapping charts, the product
is the invertible linear map that takes one to the other. The transition functions have to be consistent in the sense that if one goes to another description of the same set, and then back again, then nothing has changed. A necessary and sufficient condition for consistency is the following: Given three overlapping charts, the product 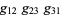 has to be the constant map to the identity in
has to be the constant map to the identity in 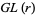 .
.
A consistent set of transition functions for a vector bundle of bundle rank 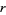 can be interpreted as an element of the first Čech cohomology group of a manifold with coefficients in
can be interpreted as an element of the first Čech cohomology group of a manifold with coefficients in 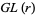 .
.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|