المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Finsler Metric |
 1823
 06:27 مساءً
date: 24-5-2021 |
Author : Iyanaga, S. and Kawada, Y. (Eds.) 
Book or Source : Finsler Spaces." §161 in Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press 
Page and Part : pp. 540-542|
Read More
Date: 13-5-2021
2993
Date: 5-6-2021
1281
Date: 3-6-2021
1542
|
A continuous real function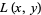 
defined on the tangent bundle 
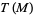of an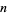 
-dimensional smooth manifold 
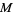is said to be a Finsler metric if
1. 
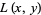is differentiable at 
,
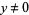2. 
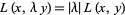for any element 
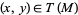and any real number 
,
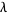3. Denoting the metric
![g_(ij)(x,y)=1/2(partial^2[L(x,y)]^2)/(partialy^ipartialy^j),](https://mathworld.wolfram.com/images/equations/FinslerMetric/NumberedEquation1.gif) |
then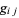 
is a positive definite matrix.
A smooth manifold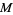 
with a Finsler metric is called a Finsler space.
REFERENCES:
Iyanaga, S. and Kawada, Y. (Eds.). "Finsler Spaces." §161 in Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press, pp. 540-542, 1980.
|
|
|
|
"عادة ليلية" قد تكون المفتاح للوقاية من الخرف
|
|
|
|
|
|
|
ممتص الصدمات: طريقة عمله وأهميته وأبرز علامات تلفه
|
|
|
|
|
|
|
الأمين العام للعتبة العسكرية المقدسة يستقبل شيوخ ووجهاء عشيرة البو بدري في مدينة سامراء
|
|
|
