
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 22-2-2021
Date: 13-4-2021
Date: 8-3-2021
|
A number 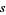 of trials in which the probability of success
of trials in which the probability of success 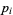 varies from trial to trial. Let
varies from trial to trial. Let  be the number of successes, then
be the number of successes, then
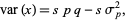 |
(1) |
where 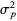 is the variance of
is the variance of 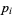 and
and 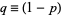 . Uspensky has shown that
. Uspensky has shown that
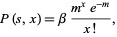 |
(2) |
where
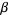 |
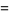 |
![[1-thetag(x)]e^(h(x))](https://mathworld.wolfram.com/images/equations/PoissonTrials/Inline9.gif) |
(3) |
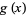 |
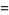 |
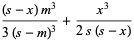 |
(4) |
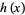 |
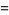 |
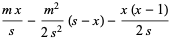 |
(5) |
 |
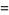 |
![p[x/2(1+1/m)-((x-m)^2)/(2m)]](https://mathworld.wolfram.com/images/equations/PoissonTrials/Inline18.gif) |
(6) |
and 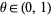 . The probability that the number of successes is at least
. The probability that the number of successes is at least  is given by
is given by
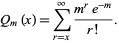 |
(7) |
Uspensky gives the true probability that there are at least  successes in
successes in 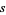 trials as
trials as
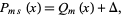 |
(8) |
where
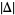 |
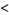 |
![{(e^chi-1)Q_m(x+1) for Q_m(x+1)>=1/2; (e^chi-1)[1-Q_m(x+1)] for Q_m(x+1)<=1/2](https://mathworld.wolfram.com/images/equations/PoissonTrials/Inline25.gif) |
(9) |
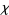 |
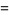 |
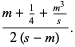 |



|
|
|
|
هل يمكن أن تكون الطماطم مفتاح الوقاية من السرطان؟
|
|
|
|
|
|
|
اكتشاف عرائس"غريبة" عمرها 2400 عام على قمة هرم بالسلفادور
|
|
|
|
|
|
|
جامعة الكفيل تقيم ندوة علمية عن الاعتماد الأكاديمي في جامعة جابر بن حيّان
|
|
|