


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 15-4-2021
Date: 30-4-2021
Date: 13-2-2021
|
The Bonferroni correction is a multiple-comparison correction used when several dependent or independent statistical tests are being performed simultaneously (since while a given alpha value 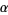 may be appropriate for each individual comparison, it is not for the set of all comparisons). In order to avoid a lot of spurious positives, the alpha value needs to be lowered to account for the number of comparisons being performed.
may be appropriate for each individual comparison, it is not for the set of all comparisons). In order to avoid a lot of spurious positives, the alpha value needs to be lowered to account for the number of comparisons being performed.
The simplest and most conservative approach is the Bonferroni correction, which sets the alpha value for the entire set of 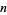 comparisons equal to
comparisons equal to 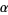 by taking the alpha value for each comparison equal to
by taking the alpha value for each comparison equal to 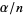 . Explicitly, given
. Explicitly, given 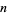 tests
tests 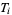 for hypotheses
for hypotheses 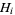 (
(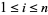 ) under the assumption
) under the assumption 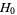 that all hypotheses
that all hypotheses 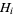 are false, and if the individual test critical values are
are false, and if the individual test critical values are 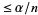 , then the experiment-wide critical value is
, then the experiment-wide critical value is 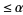 . In equation form, if
. In equation form, if
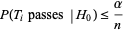 |
for 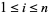 , then
, then
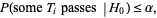 |
which follows from the Bonferroni inequalities.
REFERENCES:
Bonferroni, C. E. "Il calcolo delle assicurazioni su gruppi di teste." In Studi in Onore del Professore Salvatore Ortu Carboni. Rome: Italy, pp. 13-60, 1935.
Bonferroni, C. E. "Teoria statistica delle classi e calcolo delle probabilità." Pubblicazioni del R Istituto Superiore di Scienze Economiche e Commerciali di Firenze 8, 3-62, 1936.
Dewey, M. "Carlo Emilio Bonferroni: Life and Works." http://www.aghmed.fsnet.co.uk/bonf/bonf.html.
Miller, R. G. Jr. Simultaneous Statistical Inference. New York: Springer-Verlag, 1991.
Perneger, T. V. "What's Wrong with Bonferroni Adjustments." Brit. Med. J. 316, 1236-1238, 1998.
Shaffer, J. P. "Multiple Hypothesis Testing." Ann. Rev. Psych. 46, 561-584, 1995.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|