Skewness is a measure of the degree of asymmetry of a distribution. If the left tail (tail at small end of the distribution) is more pronounced than the right tail (tail at the large end of the distribution), the function is said to have negative skewness. If the reverse is true, it has positive skewness. If the two are equal, it has zero skewness.

Several types of skewness are defined, the terminology and notation of which are unfortunately rather confusing. "The" skewness of a distribution is defined to be

(1)

where 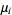 is the 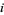th central moment. The notation  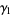is due to Karl Pearson, but the notations  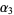(Kenney and Keeping 1951, p. 27; Kenney and Keeping 1962, p. 99) and  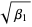(due to R. A. Fisher) are also encountered (Kenney and Keeping 1951, p. 27; Kenney and Keeping 1962, p. 99; Abramowitz and Stegun 1972, p. 928). Abramowitz and Stegun (1972, p. 928) also confusingly refer to both  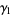and 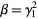 as "skewness." Skewness is implemented in the Wolfram Language as Skewness[dist].

An estimator 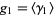 for the skewnes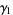s  is

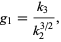(2)

where the 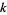s are k-statistics (Kenney and Keeping 1962, p. 101). For a normal population with a sample size of 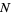, the variance of  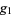is

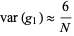(3)

(Kendall et al. 1998).

The following table gives the skewness for a number of common distributions.

distribution	skewness
Bernoulli distribution
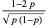Beta distribution
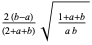binomial distribution
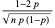chi-squared distribution
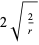exponential distribution	2
extreme value distribution
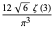F-distribution
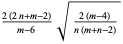gamma distribution
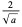geometric distribution
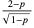half-normal distribution
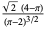hypergeometric distribution
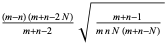Laplace distribution	0
log normal distribution
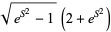Maxwell distribution
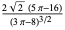negative binomial distribution
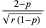normal distribution	0
Poisson distribution
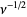Rayleigh distribution
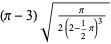Snedecor's F-distribution
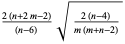Student's t-distribution	0
uniform distribution	0

Several other forms of skewness are also defined. The momental skewness is defined by

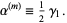(4)

The Pearson mode skewness is defined by

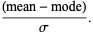(5)

Pearson's skewness coefficients are defined by

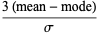(6)

and

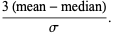(7)

The Bowley skewness (also known as quartile skewness coefficient) is defined by

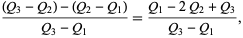(8)

where the 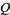s denote the interquartile ranges. The momental skewness is

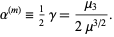(9)

REFERENCES:

Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 928, 1972.

Kendall, W. S.; Barndorff-Nielson, O.; and van Lieshout, M. C. Current Trends in Stochastic Geometry: Likelihood and Computation. Boca Raton, FL: CRC Press, 1998.

Kenney, J. F. and Keeping, E. S. "Skewness." §7.10 in Mathematics of Statistics, Pt. 1, 3rd ed. Princeton, NJ: Van Nostrand, pp. 100-101, 1962.

Kenney, J. F. and Keeping, E. S. Mathematics of Statistics, Pt. 2, 2nd ed. Princeton, NJ: Van Nostrand, 1951.

Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Moments of a Distribution: Mean, Variance, Skewness, and So Forth." §14.1 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 604-609, 1992.

Stuart, A.; and Ord, J. K. Kendall's Advanced Theory of Statistics, Vol. 1: Distribution Theory, 6th ed. New York: Oxford University Press, 1998.

اخر الاخبار

اخبار العتبة العباسية المقدسة

متحف الكفيل يباشر صيانة المجموعة الرابعة من مقتنيات العتبة العسكرية المقدسة

ضمن برنامجها التبليغي اليومي.. شعبة الخطابة تنظم مجلسًا للوعظ والإرشاد

قسم الشؤون الفكرية يواصل إقامة مسابقة النور الزكي الرمضانية في ذي قار

المجمَع العلمي يواصل إقامة 18 ختمة قرآنية رمضانية في الديوانية

المزيد

الآخبار الصحية

دراسة: تناول القهوة يوميا يخفض خطر الإصابة بالاضطرابات النفسية

عرض شائع في الفم قد يكون مرتبطا بخطر الإصابة بأمراض خطيرة

نصائح عامة لاستخدام سماعات الرأس بأمان

تأثير اللياقة البدنية على الدماغ

المزيد

الآخبار التكنلوجية

ديدان الأرض تكشف تلوث التربة بالمعادن الثقيلة

خبير أرصاد جوية: ظاهرة النينيو القادمة قد تكون الأقوى خلال 10 سنوات

"ناسا" تكشف موعد إعادة إطلاق رحلتها المأهولة إلى القمر

علماء الجيولوجيا يفكون لغز الصدع العملاق تحت الماء في المحيط الأطلسي

المزيد