


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 10-2-2021
Date: 31-3-2021
Date: 15-3-2021
|
The 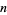 th
th 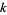 -statistic
-statistic 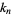 is the unique symmetric unbiased estimator of the cumulant
is the unique symmetric unbiased estimator of the cumulant 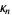 of a given statistical distribution, i.e.,
of a given statistical distribution, i.e., 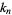 is defined so that
is defined so that
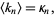 |
(1) |
where 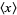 denotes the expectation value of
denotes the expectation value of  (Kenney and Keeping 1951, p. 189; Rose and Smith 2002, p. 256). In addition, the variance
(Kenney and Keeping 1951, p. 189; Rose and Smith 2002, p. 256). In addition, the variance
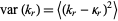 |
(2) |
is a minimum compared to all other unbiased estimators (Halmos 1946; Rose and Smith 2002, p. 256). Most authors (e.g., Kenney and Keeping 1951, 1962) use the notation 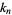 for
for 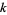 -statistics, while Rose and Smith (2002) prefer
-statistics, while Rose and Smith (2002) prefer 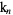 .
.
The 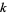 -statistics can be given in terms of the sums of the
-statistics can be given in terms of the sums of the 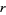 th powers of the data points as
th powers of the data points as
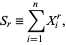 |
(3) |
then
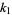 |
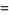 |
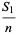 |
(4) |
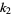 |
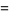 |
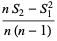 |
(5) |
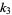 |
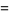 |
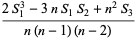 |
(6) |
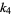 |
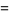 |
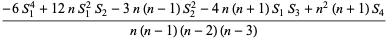 |
(7) |
(Fisher 1928; Rose and Smith 2002, p. 256). These can be given by KStatistic[r] in the Mathematica application package mathStatica.
For a sample size 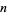 , the first few
, the first few 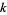 -statistics are given by
-statistics are given by
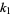 |
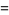 |
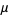 |
(8) |
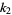 |
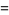 |
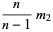 |
(9) |
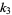 |
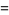 |
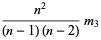 |
(10) |
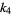 |
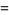 |
![(n^2[(n+1)m_4-3(n-1)m_2^2])/((n-1)(n-2)(n-3)),](https://mathworld.wolfram.com/images/equations/k-Statistic/Inline38.gif) |
(11) |
where 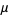 is the sample mean,
is the sample mean, 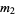 is the sample variance, and
is the sample variance, and 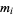 is the
is the 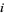 th sample central moment (Kenney and Keeping 1951, pp. 109-110, 163-165, and 189; Kenney and Keeping 1962).
th sample central moment (Kenney and Keeping 1951, pp. 109-110, 163-165, and 189; Kenney and Keeping 1962).
The variances of the first few 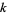 -statistics are given by
-statistics are given by
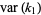 |
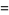 |
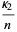 |
(12) |
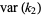 |
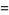 |
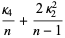 |
(13) |
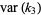 |
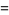 |
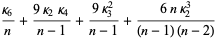 |
(14) |
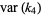 |
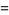 |
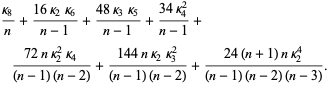 |
(15) |
An unbiased estimator for 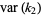 is given by
is given by
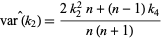 |
(16) |
(Kenney and Keeping 1951, p. 189). In the special case of a normal parent population, an unbiased estimator for 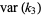 is given by
is given by
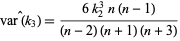 |
(17) |
(Kenney and Keeping 1951, pp. 189-190).
For a finite population, let a sample size 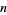 be taken from a population size
be taken from a population size 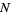 . Then unbiased estimators
. Then unbiased estimators 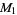 for the population mean
for the population mean 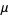 ,
, 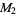 for the population variance
for the population variance 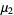 ,
, 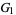 for the population skewness
for the population skewness 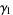 , and
, and 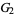 for the population kurtosis excess
for the population kurtosis excess 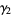 are
are
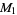 |
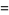 |
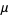 |
(18) |
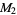 |
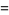 |
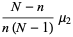 |
(19) |
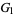 |
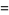 |
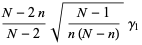 |
(20) |
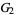 |
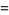 |
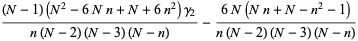 |
(21) |
(Church 1926, p. 357; Carver 1930; Irwin and Kendall 1944; Kenney and Keeping 1951, p. 143), where 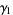 is the sample skewness and
is the sample skewness and 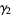 is the sample kurtosis excess.
is the sample kurtosis excess.
REFERENCES:
Carver, H. C. (Ed.). "Fundamentals of the Theory of Sampling." Ann. Math. Stat. 1, 101-121, 1930.
Church, A. E. R. "On the Means and Squared Standard-Deviations of Small Samples from Any Population." Biometrika 18, 321-394, 1926.
Fisher, R. A. "Moments and Product Moments of Sampling Distributions." Proc. London Math. Soc. 30, 199-238, 1928.
Halmos, P. R. "The Theory of Unbiased Estimation." Ann. Math. Stat. 17, 34-43, 1946.
Irwin, J. O. and Kendall, M. G. "Sampling Moments of Moments for a Finite Population." Ann. Eugenics 12, 138-142, 1944.
Kenney, J. F. and Keeping, E. S. Mathematics of Statistics, Pt. 2, 2nd ed. Princeton, NJ: Van Nostrand, 1951.
Kenney, J. F. and Keeping, E. S. "The 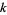 -Statistics." §7.9 in Mathematics of Statistics, Pt. 1, 3rd ed. Princeton, NJ: Van Nostrand, pp. 99-100, 1962.
-Statistics." §7.9 in Mathematics of Statistics, Pt. 1, 3rd ed. Princeton, NJ: Van Nostrand, pp. 99-100, 1962.
Rose, C. and Smith, M. D. "k-Statistics: Unbiased Estimators of Cumulants." §7.2C in Mathematical Statistics with Mathematica. New York: Springer-Verlag, pp. 256-259, 2002.
Stuart, A.; and Ord, J. K. Kendall's Advanced Theory of Statistics, Vol. 2A: Classical Inference & the Linear Model, 6th ed. New York: Oxford University Press, 1999.
Ziaud-Din, M. "Expression of the k-Statistics 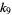 and
and 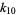 in Terms of Power Sums and Sample Moments." Ann. Math. Stat. 25, 800-803, 1954.
in Terms of Power Sums and Sample Moments." Ann. Math. Stat. 25, 800-803, 1954.
Ziaud-Din, M. "The Expression of 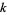 -Statistic
-Statistic 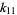 in Terms of Power Sums and Sample Moments." Ann. Math. Stat. 30, 825-828, 1959.
in Terms of Power Sums and Sample Moments." Ann. Math. Stat. 30, 825-828, 1959.
Ziaud-Din, M. and Ahmad, M. "On the Expression of the 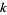 -Statistic
-Statistic 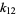 in Terms of Power Sums and Sample Moments." Bull. Internat. Stat. Inst. 38, 635-640, 1960.
in Terms of Power Sums and Sample Moments." Bull. Internat. Stat. Inst. 38, 635-640, 1960.



|
|
|
|
مخاطر خفية لمكون شائع في مشروبات الطاقة والمكملات الغذائية
|
|
|
|
|
|
|
"آبل" تشغّل نظامها الجديد للذكاء الاصطناعي على أجهزتها
|
|
|
|
|
|
|
المجمع العلميّ يُواصل عقد جلسات تعليميّة في فنون الإقراء لطلبة العلوم الدينيّة في النجف الأشرف
|
|
|