
Statistical Median
 المؤلف:
Hogg, R. V. and Craig, A.
المؤلف:
Hogg, R. V. and Craig, A.
 المصدر:
Introduction to Mathematical Statistics, 5th ed. New York: Macmillan, 1995
المصدر:
Introduction to Mathematical Statistics, 5th ed. New York: Macmillan, 1995
 الجزء والصفحة:
...
الجزء والصفحة:
...
 10-2-2021
10-2-2021
 4006
4006
Statistical Median
The median of a statistical distribution with distribution function 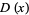 is the value
is the value  such
such 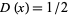 . For a symmetric distribution, it is therefore equal to the mean.
. For a symmetric distribution, it is therefore equal to the mean.
Given order statistics 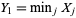 ,
, 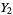 , ...,
, ..., 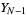 ,
, 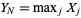 , the statistical median of the random sample is defined by
, the statistical median of the random sample is defined by
![x^~=<span style=]() {Y_((N+1)/2) if N is odd; 1/2(Y_(N/2)+Y_(1+N/2)) if N is even " src="https://mathworld.wolfram.com/images/equations/StatisticalMedian/NumberedEquation1.gif" style="height:50px; width:210px" /> {Y_((N+1)/2) if N is odd; 1/2(Y_(N/2)+Y_(1+N/2)) if N is even " src="https://mathworld.wolfram.com/images/equations/StatisticalMedian/NumberedEquation1.gif" style="height:50px; width:210px" /> |
(1)
|
(Hogg and Craig 1995, p. 152) and commonly denoted 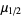 or
or  . The median of a list of data is implemented as Median[list].
. The median of a list of data is implemented as Median[list].
For a normal population, the mean 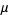 is the most efficient (in the sense that no other unbiased statistic for estimating
is the most efficient (in the sense that no other unbiased statistic for estimating 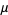 can have smaller variance) estimate (Kenney and Keeping 1962, p. 211). The efficiency of the median, measured as the ratio of the variance of the mean to the variance of the median, depends on the sample size
can have smaller variance) estimate (Kenney and Keeping 1962, p. 211). The efficiency of the median, measured as the ratio of the variance of the mean to the variance of the median, depends on the sample size 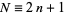 as
as
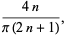 |
(2)
|
which tends to the value 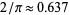 as
as 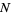 becomes large (Kenney and Keeping 1962, p. 211). Although, the median is less efficient than the mean, it is less sensitive to outliers than the mean
becomes large (Kenney and Keeping 1962, p. 211). Although, the median is less efficient than the mean, it is less sensitive to outliers than the mean
For large 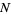 samples with population median
samples with population median 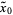 ,
,
The median is an L-estimate (Press et al. 1992).
An interesting empirical relationship between the mean, median, and mode which appears to hold for unimodal curves of moderate asymmetry is given by
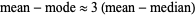 |
(5)
|
(Kenney and Keeping 1962, p. 53), which is the basis for the definition of the Pearson mode skewness.
REFERENCES:
Hogg, R. V. and Craig, A. T. Introduction to Mathematical Statistics, 5th ed. New York: Macmillan, 1995.
Huang, J. S. "Third-Order Expansion of Mean Squared Error of Medians." Stat. Prob. Let. 42, 185-192, 1999.
Kenney, J. F. and Keeping, E. S. "The Median," "Relation Between Mean, Median, and Mode," "Relative Merits of Mean, Median, and Mode," and "The Median." §3.2, 4.8-4.9, and 13.13 in Mathematics of Statistics, Pt. 1, 3rd ed. Princeton, NJ: Van Nostrand, pp. 32-35, 52-54, 211-212, 1962.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, p. 694, 1992.
Zwillinger, D. (Ed.). CRC Standard Mathematical Tables and Formulae. Boca Raton, FL: CRC Press, p. 602, 1995.
 الاكثر قراءة في الاحتمالات و الاحصاء
الاكثر قراءة في الاحتمالات و الاحصاء
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


