
Liouville,s Constant
 المؤلف:
Apostol, T. M.
المؤلف:
Apostol, T. M.
 المصدر:
Modular Functions and Dirichlet Series in Number Theory, 2nd ed. New York: Springer-Verlag
المصدر:
Modular Functions and Dirichlet Series in Number Theory, 2nd ed. New York: Springer-Verlag
 الجزء والصفحة:
...
الجزء والصفحة:
...
 1-2-2021
1-2-2021
 3451
3451
Liouville's Constant
Liouville's constant, sometimes also called Liouville's number, is the real number defined by
(OEIS A012245). Liouville's constant is a decimal fraction with a 1 in each decimal place corresponding to a factorial 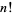 , and zeros everywhere else. Liouville (1844) constructed an infinite class of transcendental numbers using continued fractions, but the above number was the first decimal constant to be proven transcendental (Liouville 1850). However, Cantor subsequently proved that "almost all" real numbers are in fact transcendental.
, and zeros everywhere else. Liouville (1844) constructed an infinite class of transcendental numbers using continued fractions, but the above number was the first decimal constant to be proven transcendental (Liouville 1850). However, Cantor subsequently proved that "almost all" real numbers are in fact transcendental.
A recurrence plot of the binary digits is illustrated above.
Liouville's constant nearly satisfies
which has solution 0.1100009999... (OEIS A093409), but plugging 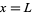 into this equation gives
into this equation gives 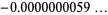 instead of 0.
instead of 0.
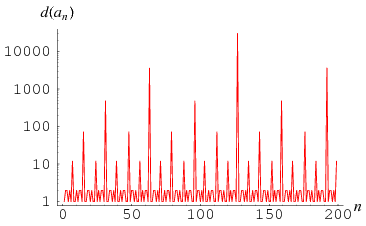
Liouville's constant has continued fraction [0, 9, 11, 99, 1, 10, 9, 999999999999, 1, 8, 10, 1, 99, 11, 9, 999999999999999999999999999999999999999999999999999999999999999999999999, ...] (OEIS A058304; Stark 1994, pp. 172-177), which shows sporadic large terms. The numbers of digits 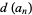 in the
in the 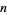 th term is plotted above on a semilog plot, which shows a nested structure (E. Zeleny, pers. comm., Aug. 17, 2005). Interestingly, the
th term is plotted above on a semilog plot, which shows a nested structure (E. Zeleny, pers. comm., Aug. 17, 2005). Interestingly, the  th incrementally largest term (considering only those entirely of 9s in order to exclude the term
th incrementally largest term (considering only those entirely of 9s in order to exclude the term 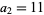 ) occurs precisely at position
) occurs precisely at position 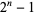 , and this term consists of
, and this term consists of 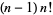 9s.
9s.
REFERENCES:
Apostol, T. M. Modular Functions and Dirichlet Series in Number Theory, 2nd ed. New York: Springer-Verlag, p. 147, 1997.
Conway, J. H. and Guy, R. K. "Liouville's Number." In The Book of Numbers. New York: Springer-Verlag, pp. 239-241, 1996.
Courant, R. and Robbins, H. "Liouville's Theorem and the Construction of Transcendental Numbers." §2.6.2 in What Is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed. Oxford, England: Oxford University Press, pp. 104-107, 1996.
Liouville, J. "Mémoires et communications des Membres et des correspondants de l'Académie." C. R. Acad. Sci. Paris 18, 883-885, 1844.
Liouville, J. "Nouvelle démonstration d'un théor'eme sur les irrationalles algébriques, inséré dans le Compte rendu de la dernière séance." C. R. Acad. Sci. Paris 18, 910-911, 1844.
Liouville, J. "Sur des classes très-étendues de quantités dont la valeur n'est ni algébrique, ni même réductible à des irrationelles algébriques." J. Math. pures appl. 16, 133-142, 1851.
Sloane, N. J. A. Sequences A012245, A058304, and A093409 in "The On-Line Encyclopedia of Integer Sequences."
Stark, H. M. An Introduction to Number Theory. Cambridge, MA: MIT Press, 1994.
Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, p. 26, 1986.
 الاكثر قراءة في نظرية الاعداد
الاكثر قراءة في نظرية الاعداد
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


