
Pseudoprime
 المؤلف:
Caldwell, C. K.
المؤلف:
Caldwell, C. K.
 المصدر:
"Prime Links++." http://primes.utm.edu/links/theory/finding_and_proving/probable_primality/.
المصدر:
"Prime Links++." http://primes.utm.edu/links/theory/finding_and_proving/probable_primality/.
 الجزء والصفحة:
...
الجزء والصفحة:
...
 25-1-2021
25-1-2021
 1230
1230
Pseudoprime
A pseudoprime is a composite number that passes a test or sequence of tests that fail for most composite numbers. Unfortunately, some authors drop the "composite" requirement, calling any number that passes the specified tests a pseudoprime even if it is prime. Pomerance, Selfridge, and Wagstaff (1980) restrict their use of "pseudoprime" to odd composite numbers.
"Pseudoprime" used without qualification means Fermat pseudoprime, i.e., a composite number that nonetheless satisfies Fermat's little theorem to some base or set of bases.
Carmichael numbers are odd composite numbers that are Fermat pseudoprimes to every base; they are sometimes called absolute pseudoprimes.
The following table gives the number of Poulet numbers psp(2), Euler-Jacobi pseudoprimes ejpsp(2), and strong pseudoprimes spsp(2) to the base 2, and Carmichael numbers CN that are smaller than the first few powers of 10 (Guy 1994). The table below extend Guy's table with the results of Pinch, who calculated the number of pseudoprimes up to 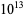 .
.
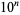 |
psp(2) |
ejpsp(2) |
spsp(2) |
CN |
| Sloane |
A055550 |
A055551 |
A055552 |
A055553 |
| Sloane counts |
A001567 |
A047713 |
A001262 |
A002997 |
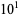 |
0 |
0 |
0 |
0 |
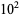 |
0 |
0 |
0 |
0 |
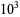 |
3 |
1 |
0 |
1 |
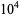 |
22 |
12 |
5 |
7 |
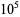 |
78 |
36 |
16 |
16 |
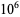 |
245 |
114 |
46 |
43 |
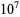 |
750 |
375 |
162 |
105 |
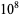 |
2057 |
1071 |
488 |
255 |
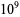 |
5597 |
2939 |
1282 |
646 |
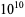 |
14884 |
7706 |
3291 |
1547 |
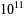 |
38975 |
20417 |
8607 |
3605 |
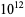 |
101629 |
53332 |
22407 |
8241 |
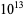 |
264239 |
124882 |
58892 |
19279 |
REFERENCES:
Caldwell, C. K. "Prime Links++." http://primes.utm.edu/links/theory/finding_and_proving/probable_primality/.
Grantham, J. "Frobenius Pseudoprimes." http://www.clark.net/pub/grantham/pseudo/pseudo1.ps.
Grantham, J. "Pseudoprimes/Probable Primes." http://www.clark.net/pub/grantham/pseudo/.
Guy, R. K. "Pseudoprimes. Euler Pseudoprimes. Strong Pseudoprimes." §A12 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 27-30, 1994.
Pinch, R. G. E. "The Pseudoprimes Up to 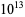 ." ftp://ftp.dpmms.cam.ac.uk/pub/PSP/.
." ftp://ftp.dpmms.cam.ac.uk/pub/PSP/.
Pomerance, C.; Selfridge, J. L.; and Wagstaff, S. S. Jr. "The Pseudoprimes to 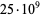 ." Math. Comput. 35, 1003-1026, 1980. http://mpqs.free.fr/ThePseudoprimesTo25e9.pdf.
." Math. Comput. 35, 1003-1026, 1980. http://mpqs.free.fr/ThePseudoprimesTo25e9.pdf.
Sloane, N. J. A. Sequences A001262, A001567/M5441, A002997/M5462, A047713, A055550, A055551, A055552, and A055553 in "The On-Line Encyclopedia of Integer Sequences."
 الاكثر قراءة في نظرية الاعداد
الاكثر قراءة في نظرية الاعداد
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


