
Smooth Number
 المؤلف:
Blecksmith, R.; McCallum, M.; and Selfridge, J. L.
المؤلف:
Blecksmith, R.; McCallum, M.; and Selfridge, J. L.
 المصدر:
"3-Smooth Representations of Integers." Amer. Math. Monthly 105,
المصدر:
"3-Smooth Representations of Integers." Amer. Math. Monthly 105,
 الجزء والصفحة:
...
الجزء والصفحة:
...
 21-1-2021
21-1-2021
 1004
1004
Smooth Number
An integer is 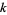 -smooth if it has no prime factors
-smooth if it has no prime factors 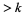 . The following table gives the first few
. The following table gives the first few 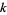 -smooth numbers for small
-smooth numbers for small 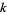 . Berndt (1994, p. 52) called the 7-smooth numbers "highly composite numbers."
. Berndt (1994, p. 52) called the 7-smooth numbers "highly composite numbers."
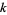 |
OEIS |
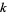 -smooth numbers -smooth numbers |
| 2 |
A000079 |
1, 2, 4, 8, 16, 32, 64, 128, 256, 512, ... |
| 3 |
A003586 |
1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, ... |
| 5 |
A051037 |
1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 16, ... |
| 7 |
A002473 |
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 14, 15, ... |
| 11 |
A051038 |
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 14, ... |
The probability that a random positive integer 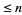 is
is 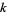 -smooth is
-smooth is 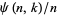 , where
, where 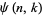 is the number of
is the number of 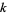 -smooth numbers
-smooth numbers 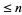 . This fact is important in application of Kraitchik's extension of Fermat's factorization method because it is related to the number of random numbers which must be examined to find a suitable subset whose product is a square.
. This fact is important in application of Kraitchik's extension of Fermat's factorization method because it is related to the number of random numbers which must be examined to find a suitable subset whose product is a square.
Since about 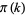
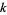 -smooth numbers must be found (where
-smooth numbers must be found (where 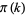 is the prime counting function), the number of random numbers which must be examined is about
is the prime counting function), the number of random numbers which must be examined is about 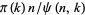 . But because it takes about
. But because it takes about 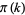 steps to determine if a number is
steps to determine if a number is 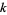 -smooth using trial division, the expected number of steps needed to find a subset of numbers whose product is a square is
-smooth using trial division, the expected number of steps needed to find a subset of numbers whose product is a square is ![∼[pi(k)]^2n/psi(n,k)](https://mathworld.wolfram.com/images/equations/SmoothNumber/Inline19.gif) (Pomerance 1996). Canfield et al. (1983) showed that this function is minimized when
(Pomerance 1996). Canfield et al. (1983) showed that this function is minimized when
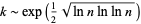 |
(1)
|
and that the minimum value is about
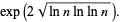 |
(2)
|
In the continued fraction factorization algorithm, 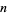 can be taken as
can be taken as 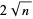 , but in Fermat's factorization method, it is
, but in Fermat's factorization method, it is 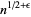 .
. 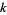 is an estimate for the largest prime in the factor base (Pomerance 1996).
is an estimate for the largest prime in the factor base (Pomerance 1996).
The curiosity
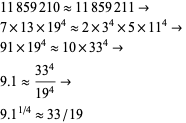 |
(3)
|
involves the largest consecutive 19-smooth numbers, 11859210 and 11859211.
REFERENCES:
Berndt, B. C. Ramanujan's Notebooks, Part IV. New York: Springer-Verlag, 1994.
Blecksmith, R.; McCallum, M.; and Selfridge, J. L. "3-Smooth Representations of Integers." Amer. Math. Monthly 105, 529-543, 1998.
Canfield, E. R.; Erdős, P.; and Pomerance, C. "On a Problem of Oppenheim Concerning 'Factorisation Numerorum.' " J. Number Th. 17, 1-28, 1983.
Mintz, D. J. "2, 3 Sequence as a Binary Mixture." Fib. Quart. 19, 351-360, 1981.
Pomerance, C. "On the Role of Smooth Numbers in Number Theoretic Algorithms." In Proc. Internat. Congr. Math., Zürich, Switzerland, 1994, Vol. 1 (Ed. S. D. Chatterji). Basel: Birkhäuser, pp. 411-422, 1995.
Pomerance, C. "A Tale of Two Sieves." Not. Amer. Math. Soc. 43, 1473-1485, 1996.
Ramanujan, S. Collected Papers of Srinivasa Ramanujan (Ed. G. H. Hardy, P. V. S. Aiyar, and B. M. Wilson). Providence, RI: Amer. Math. Soc., p. xxiv, 2000.
Sloane, N. J. A. Sequences A000079/M1129, A002473/M0477, A003586, A051037, and A051038 in "The On-Line Encyclopedia of Integer Sequences."
 الاكثر قراءة في نظرية الاعداد
الاكثر قراءة في نظرية الاعداد
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


