Mersenne Prime

A Mersenne prime is a Mersenne number, i.e., a number of the form

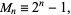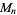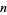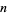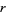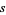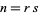that is prime. In order for  to be prime,  must itself be prime. This is true since for composite  with factors  and , . Therefore,  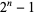can be written as 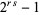, which is a binomial number that always has a factor .

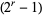The first few Mersenne primes are 3, 7, 31, 127, 8191, 131071, 524287, 2147483647, ... (OEIS A000668) corresponding to indices 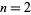, 3, 5, 7, 13, 17, 19, 31, 61, 89, ... (OEIS A000043).

Mersenne primes were first studied because of the remarkable properties that every Mersenne prime corresponds to exactly one perfect number. L. Welsh maintains an extensive bibliography and history of Mersenne numbers.

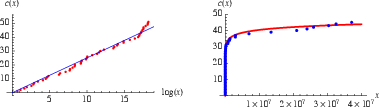
It has been conjectured that there exist an infinite number of Mersenne primes. Fitting a line through the origin to the asymptotic number of Mersenne primes 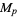 with 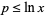 for the first 51 (known) Mersenne primes gives a best-fit line with 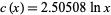, illustrated above. If the line is not restricted to pass through the origin, the best fit is . It has been conjectured (without any particularly strong evidence) that the constant is given by , where  is the Euler-Mascheroni constant (Havil 2003, p. 116; Caldwell), a result related to Wagstaff's conjecture

However, finding Mersenne primes is computationally very challenging. For example, the 1963 discovery that 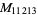 is prime was heralded by a special postal meter design, illustrated above, issued in Urbana, Illinois.

G. Woltman has organized a distributed search program via the Internet known as GIMPS (Great Internet Mersenne Prime Search) in which hundreds of volunteers use their personal computers to perform pieces of the search. The efforts of GIMPS volunteers make this distributed computing project the discoverer of all of the Mersenne primes discovered since late 1996. As of Sep. 24, 2020, GIMPS participants have tested and verified all exponents below 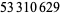 and tested all exponents below  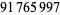at least once (GIMPS).

The table below gives the index 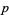 of known Mersenne primes (OEIS A000043) 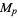, together with the number of digits, discovery years, and discoverer. A similar table has been compiled by C. Caldwell. Note that sequential indexing of "the" 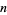th Mersenne prime is tentative for  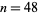until all exponents between  and 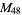 (namely up to 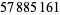) have been verified to be composite (and therefore also tentative for the other known Mersenne primes  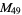through ).

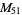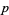#		digits	year	discoverer (reference)	value
1	2	1	antiquity		3
2	3	1	antiquity		7
3	5	2	antiquity		31
4	7	3	antiquity		127
5	13	4	1461	Reguis (1536), Cataldi (1603)	8191
6	17	6	1588	Cataldi (1603)	131071
7	19	6	1588	Cataldi (1603)	524287
8	31	10	1750	Euler (1772)	2147483647
9	61	19	1883	Pervouchine (1883), Seelhoff (1886)	2305843009213693951
10	89	27	1911	Powers (1911)	618970019642690137449562111
11	107	33	1913	Powers (1914)	162259276829213363391578010288127
12	127	39	1876	Lucas (1876)	170141183460469231731687303715884105727
13	521	157	Jan. 30, 1952	Robinson (1954)	68647976601306097149...12574028291115057151
14	607	183	Jan. 30, 1952	Robinson (1954)	53113799281676709868...70835393219031728127
15	1279	386	Jun. 25, 1952	Robinson (1954)	10407932194664399081...20710555703168729087
16	2203	664	Oct. 7, 1952	Robinson (1954)	14759799152141802350...50419497686697771007
17	2281	687	Oct. 9, 1952	Robinson (1954)	44608755718375842957...64133172418132836351
18	3217	969	Sep. 8, 1957	Riesel	25911708601320262777...46160677362909315071
19	4253	1281	Nov. 3, 1961	Hurwitz	19079700752443907380...76034687815350484991
20	4423	1332	Nov. 3, 1961	Hurwitz	28554254222827961390...10231057902608580607
21	9689	2917	May 11, 1963	Gillies (1964)	47822027880546120295...18992696826225754111
22	9941	2993	May 16, 1963	Gillies (1964)	34608828249085121524...19426224883789463551
23	11213	3376	Jun. 2, 1963	Gillies (1964)	28141120136973731333...67391476087696392191
24	19937	6002	Mar. 4, 1971	Tuckerman (1971)	43154247973881626480...36741539030968041471
25	21701	6533	Oct. 30, 1978	Noll and Nickel (1980)	44867916611904333479...57410828353511882751
26	23209	6987	Feb. 9, 1979	Noll (Noll and Nickel 1980)	40287411577898877818...36743355523779264511
27	44497	13395	Apr. 8, 1979	Nelson and Slowinski	85450982430363380319...44867686961011228671
28	86243	25962	Sep. 25, 1982	Slowinski	53692799550275632152...99857021709433438207
29	110503	33265	Jan. 28, 1988	Colquitt and Welsh (1991)	52192831334175505976...69951621083465515007
30	132049	39751	Sep. 20, 1983	Slowinski	51274027626932072381...52138578455730061311
31	216091	65050	Sep. 6, 1985	Slowinski	74609310306466134368...91336204103815528447
32	756839	227832	Feb. 19, 1992	Slowinski and Gage	17413590682008709732...02603793328544677887
33	859433	258716	Jan. 10, 1994	Slowinski and Gage	12949812560420764966...02414267243500142591
34	1257787	378632	Sep. 3, 1996	Slowinski and Gage	41224577362142867472...31257188976089366527
35	1398269	420921	Nov. 12, 1996	Joel Armengaud/GIMPS	81471756441257307514...85532025868451315711
36	2976221	895832	Aug. 24, 1997	Gordon Spence/GIMPS	62334007624857864988...76506256743729201151
37	3021377	909526	Jan. 27, 1998	Roland Clarkson/GIMPS	12741168303009336743...25422631973024694271
38	6972593	2098960	Jun. 1, 1999	Nayan Hajratwala/GIMPS	43707574412708137883...35366526142924193791
39	13466917	4053946	Nov. 14, 2001	Michael Cameron/GIMPS	92494773800670132224...30073855470256259071
40	20996011	6320430	Nov. 17, 2003	Michael Shafer/GIMPS	12597689545033010502...94714065762855682047
41	24036583	7235733	May 15, 2004	Josh Findley/GIMPS	29941042940415717208...67436921882733969407
42	25964951	7816230	Feb. 18, 2005	Martin Nowak/GIMPS	12216463006127794810...98933257280577077247
43	30402457	9152052	Dec. 15, 2005	Curtis Cooper and Steven Boone/GIMPS	31541647561884608093...11134297411652943871
44	32582657	9808358	Sep. 4, 2006	Curtis Cooper and Steven Boone/GIMPS	12457502601536945540...11752880154053967871
45	37156667	11185272	Sep. 6, 2008	Hans-Michael Elvenich/GIMPS	20225440689097733553...21340265022308220927
46	42643801	12837064	Jun. 12, 2009	Odd Magnar Strindmo/GIMPS	16987351645274162247...84101954765562314751
47	43112609	12978189	Aug. 23, 2008	Edson Smith/GIMPS	31647026933025592314...80022181166697152511
48?	57885161	17425170	Jan. 25, 2013	Curtis Cooper/GIMPS	58188726623224644217...46141988071724285951
49?	74207281	22338618	Jan. 7, 2016	Curtis Cooper/GIMPS	30037641808460618205...87010073391086436351
50?	77232917	23249425	Dec. 26, 2017	Jonathan Pace/GIMPS	46733318335923109998...82730618069762179071
51?	82589933	24862048	Dec. 7, 2018	Patrick Laroche/GIMPS	14889444574204132554...37951210325217902591

Trial division is often used to establish the compositeness of a potential Mersenne prime. This test immediately shows 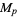 to be composite for 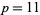, 23, 83, 131, 179, 191, 239, and 251 (with small factors 23, 47, 167, 263, 359, 383, 479, and 503, respectively). A much more powerful primality test for  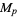is the Lucas-Lehmer test.

If 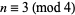 is a prime, then  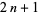divides  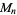iff 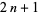 is prime. It is also true that prime divisors of  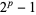must have the form  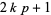where 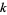 is a positive integer and simultaneously of either the form  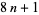or 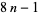 (Uspensky and Heaslet 1939).

A prime factor 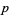 of a Mersenne number  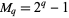is a Wieferich prime iff 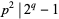. Therefore, Mersenne primes are not Wieferich primes.

REFERENCES:

Bateman, P. T.; Selfridge, J. L.; and Wagstaff, S. S. "The New Mersenne Conjecture." Amer. Math. Monthly 96, 125-128, 1989.

Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, p. 66, 1987.

Beiler, A. H. Ch. 3 in Recreations in the Theory of Numbers: The Queen of Mathematics Entertains. New York: Dover, 1966.

Bell, E. T. Mathematics: Queen and Servant of Science. Washington, DC: Math. Assoc. Amer., 1987.

Caldwell, C. "Mersenne Primes: History, Theorems and Lists." http://www.utm.edu/research/primes/mersenne/.

Caldwell, C. K. "The Top Twenty: Mersenne Primes." http://www.utm.edu/research/primes/lists/top20/Mersenne.html.

Caldwell, C. "Where Is the Next Mersenne Prime?" http://primes.utm.edu/notes/faq/NextMersenne.html.

Colquitt, W. N. and Welsh, L. Jr. "A New Mersenne Prime." Math. Comput. 56, 867-870, 1991.

Conway, J. H. and Guy, R. K. "Mersenne's Numbers." In The Book of Numbers. New York: Springer-Verlag, pp. 135-137, 1996.

Devlin, K. "World's Largest Prime." FOCUS: Newsletter Math. Assoc. Amer. 17, 1, Dec. 1997.

Dickson, L. E. History of the Theory of Numbers, Vol. 1: Divisibility and Primality. New York: Dover, p. 13, 2005.

Flannery, S. and Flannery, D. In Code: A Mathematical Journey. London: Profile Books, pp. 47-51, 2000.

Gardner, M. The Sixth Book of Mathematical Games from Scientific American. Chicago, IL: University of Chicago Press, p. 85, 1984.

Gardner, M. "Patterns in Primes Are a Clue to the Strong Law of Small Numbers." Sci. Amer. 243, 18-28, Dec. 1980.

Gillies, D. B. "Three New Mersenne Primes and a Statistical Theory." Math Comput. 18, 93-97, 1964.

GIMPS. "GIMPS Milestones Report." http://v5www.mersenne.org/report_milestones/.

Great Internet Prime Search: GIMPS. Finding World World Primes Since 1996. "List of Known Mersenne Prime Numbers." http://www.mersenne.org/primes/.

Guy, R. K. "Mersenne Primes. Repunits. Fermat Numbers. Primes of Shape 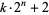 [sic]." §A3 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 8-13, 1994.

Haghighi, M. "Computation of Mersenne Primes Using a Cray X-MP." Intl. J. Comput. Math. 41, 251-259, 1992.

Hardy, G. H. and Wright, E. M. An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, pp. 14-16, 1979.

Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, 2003.

Kraitchik, M. "Mersenne Numbers and Perfect Numbers." §3.5 in Mathematical Recreations. New York: W. W. Norton, pp. 70-73, 1942.

Kravitz, S. and Berg, M. "Lucas' Test for Mersenne Numbers 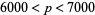." Math. Comput. 18, 148-149, 1964.

Lehmer, D. H. "On Lucas's Test for the Primality of Mersenne's Numbers." J. London Math. Soc. 10, 162-165, 1935.

Leyland, P. http://research.microsoft.com/~pleyland/factorization/factors/mersenne.txt.

Mersenne, M. Cogitata Physico-Mathematica. 1644.

Noll, C. and Nickel, L. "The 25th and 26th Mersenne Primes." Math. Comput. 35, 1387-1390, 1980.

Powers, R. E. "The Tenth Perfect Number." Amer. Math. Monthly 18, 195-196, 1911.

Powers, R. E. "Note on a Mersenne Number." Bull. Amer. Math. Soc. 40, 883, 1934.

Robinson, R. M. "Mersenne and Fermat Numbers." Proc. Amer. Math. Soc. 5, 842-846, 1954.

Shankland, S. "Cooperative Computing Finds Top Prime Number." ZDNet News: Hardware. Dec. 2, 2003. http://zdnet.com.com/2100-1103_2-5112827.html?tag=zdfd.newsfeed.

Sloane, N. J. A. Sequences A000043/M0672 and A000668/M2696 in "The On-Line Encyclopedia of Integer Sequences."

Slowinski, D. "Searching for the 27th Mersenne Prime." J. Recreat. Math. 11, 258-261, 1978-1979.

Tuckerman, B. "The 24th Mersenne Prime." Proc. Nat. Acad. Sci. USA 68, 2319-2320, 1971.

Uhler, H. S. "A Brief History of the Investigations on Mersenne Numbers and the Latest Immense Primes." Scripta Math. 18, 122-131, 1952.

Uspensky, J. V. and Heaslet, M. A. Elementary Number Theory. New York: McGraw-Hill, 1939.

Welsh, L. "Marin Mersenne." http://www.utm.edu/research/primes/mersenne/LukeMirror/mersenne.htm.

Welsh, L. "Mersenne Numbers & Mersenne Primes Bibliography." http://www.utm.edu/research/primes/mersenne/LukeMirror/biblio.htm.

Whitehouse, D. "Number Takes Prime Position." December 5, 2001. BBC News online. http://news.bbc.co.uk/hi/english/sci/tech/newsid_1693000/1693364.stm.

Woltman, G. "The GREAT Internet Mersenne Prime Search." http://www.mersenne.org/prime.htm.